76. A feladat állítása következik az

a^.(a + 2)³ – (a + 1)^.(a – 1)³ = (2a + 1)³

azonosságból.

77. El lehet. Bármely lap 4 csúcsában összesen 18 gramm súlynak kell lennie. Bő­veb­ben lásd a Bergengóc példatárban a 89. feladat megoldását a 164. oldalon!

78. Legyen vizsgált ABC háromszögünk súlypontja S, köréírt körének középpontja O. Az ACB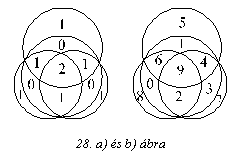 szögfelezőjének és a körülírt körnek a C-től különböző metszéspontját jelölje D. Ez a D pont a c-t nem tartalmazó AB ív felezőpontja. Az S középpontú (-½) arányú középpontos hasonlóságnál a körülírható kör képe az ABC háromszög oldalfelezőpontjain halad át. E körből az OD szakasz kimetszi AB felező­pontját. Innentől már egyszerűen megy a szerkesztés.

79. A 370 és a 371.

80. a)3997/3986 b)996 002.

81.

.

Nem lehet mindig. Erre egy példa látható a 27. áb­rán, ahol pontok jelölik a hercegségeket, és szakaszt húztunk a baráti hercegségek között.

82. Az alábbi három számpárra teljesül a megadott összefüggés:

(1993; 1993), (997^.1993; 997), (997; 997^.1993).

83. A kezdő nyer, ha elsőre a 49. mezőre lép, és azután is mindig a lehető legnagyobb sorszámú mezőt választja.

84. Nincs ilyen szám.

85. A feladat szövegéből következik, hogy BAC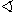 és ABC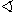hegyesszögek. Állítsunk merőlegest a B pontban az AB egyenesre! Messe ez a merőleges az AC oldal meg­hosszab­bítását az F pontban! Bizonyítsuk be[1], hogy CF = AB! Mutassuk meg, hogy a BO > AO, illetve a BO < AO egyenlőtlenség ekvivalens a BC > AC, illetve a BC < AC egyenlőtlenséggel! Húzzuk még be az ABF derékszögű háromszög BM? súlyvonalát, ez természetesen egyenlő hosszú az AM? és a BM? szakasszal. Ezért, ha az ABC háromszög leghosszabb oldala AB, akkor BC > BM? – M?C = AM? – M?C = AC, ha pedig AB a legrövidebb oldal, akkor BC < BM? + M?C = AM? + M?C = AC.

86. 8 db 5 egység hosszúból ki lehet rakni, 5 db 8 egység hosszúból nem lehet kirakni. Bővebben lásd a Bergengóc példatárban az 55. feladat megoldását a 106. oldalon.

87. 4-et kapott maradékul.

88. Nem lehet. Ehhez elég megmutatni, hogy ha a P egészegyütthatós polinomnak az m (egész) helyen felvett P(m) értéke osztható 3-mal, akkor P(m + 3k) is osztható 3-mal, bármely egész számot jelöl is k.

89. A büntetések összegének oszthatónak kell lennie 9-cel, így az elveszett bankó csak egy 5 000-es lehetett.

90. Csak nulla lehet a közös összeg. Színezzük a táblázat mezőit sakktáblaszerűen és számítsuk ki a fehér mezőkbe írt számok összegét. Kétféle átlóirány van. Az egyik irányban öt, a másikban hat átló adja ki az összes fehér mezőt. Az egyes átlókban álló számok összege csak úgy lehet egymással ha ez az összeg 0. Egy megfelelő kitöltést kapunk, ha minden mezőbe 0-t írunk.

91. Az első szám a nagyobb. A bizonyításhoz az első számot érdemes az alábbi alakba írni: (1^.1993)^.(3^.1991)^.(5^.1989)^....^.(1991^.3)^.(1993^.1).

92.

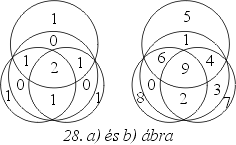
Legfeljebb 25 lehet az összeg. Legyen x az egyes körökön belüli számok –egyenlőnek feltételezett- összege. Jelölje K a középső kört, azaz azt, amelyik három helyen is átmegy másik két kör metszéspontján. Adjuk össze a másik három körbe írt számok összegeit és vonjuk ki ebből a K-ba írt számok összegét. Az így kapott szám természetesen 2x lesz. Másrészt az egyes tartományokba írt számokat ilyenkor annyiszor számoltuk, amilyen számot a megfelelő tartományban látható a 28. a) ábrán. Így becslést adhatunk: 2x £ 2^.9 + 8 + 7 + 6 + 5 + 4 + 3 = 51, azaz x £ 25. Ez a fölső határ elérhető, amint az a 28. b) ábrán bemutatott példán is látható.

93. Csak AB = BC lehet a két egyenlő oldal a háromszögben. Innen a szögek számolásával, egyenlőszárú háromszögek keresésével kapjuk, hogy a keresett szög 60^o-os.

94. Ilyen szám pld. a 999...99, azaz bármely 10^k- 1 (k > 0) alakú szám, mert négyzete 10^2k - 2^.10^k + 1 = 999...99800...01, amely (k – 1) db 9-esből és egy-egy 8-asból és 1-esből áll a nullákon kívül.

95. 16-16 figura elhelyezhető a kívánt módon.