Az 1992/93. tanév
52. Ha aranytallérokat ásol el a
Csodaréten, akkor reggelre mindegyik tallérból egy-egy fácska nő ki,
minden fán minden levél egy-egy aranytallér, mindegyik fán minden
reggel ugyanannyi tallér. Boldizsár is eljött nehezen gyűjtött
öt aranytallérjával egy pénteki napon a Csodarétre,
hogy meggazdagodjék. Azt szerette volna, hogy legalább 1992
aranytallérja legyen. Amint kinőttek az első fák, Boldizsár rájött,
hogy szerdánál előbb nem teljesülhet a vágya, de pénteknél
tovább se kell várnia. Lehetséges-e, hogy végül épp 1992
aranytallérja lett?
Megoldás
53. Bizonyítsd be, hogy ha az
a,
b,
c egész számokra teljesül az
ab + bc + ca = 0
összefüggés, akkor az
abc szorzat
fölírható egy négyzetszám és egy köbszám szorzataként!
Megoldás
54. Az
n egység
oldalú szabályos háromszöget az oldalaival párhuzamos
egyenesekkel 1 egység oldalú szabályos háromszögekre
bontottuk fel. Hány olyan szabályos háromszög van, amelynek
csúcsai a létrejött háló rácspontjai között vannak?
Megoldás
55. A rozmár, a víziló, a pelikán
és a bálna összesen 37 halat ettek meg. A bálna épp annyiszor
több halat evett a pelikánnál, mint ahányszor többet evett
a pelikán a rozmárnál. Mennyi halat ettek meg külön-külön?
Megoldás
56. Az
M pontot az
ABC
háromszög belsejében vettük fel. Legyen
L az
M
pontot a háromszög csúcsaival összekötő szakaszok
közül a legnagyobb,
l pedig
M-et a
háromszög oldalfelezőpontjaival összekötő
szakaszok közül a legkisebb. Bizonyítsd be, hogy
L 2
l
!
Megoldás
57. Egy röplabdabajnokságban
mindenki mindenkivel pontosan egyszer játszott. A verseny végén
kiderült, hogy mindegyik csapat épp annyi mérkőzést nyert meg,
mint ahányat az őt legyőző csapatok összesen nyertek. Hány
csapat vett részt a bajnokságban?
Megoldás
58. 1988-ban kezdte el vetíteni a
Bergengóc Televízió a “Térdig könnyben” című
sorozatot. 1989-től minden évben vagy 40%-kal több, vagy 40%-kal
kevesebb részt mutattak be, mint az előző évben. Hogy az ország
gazdaságát ne tegyék teljesen tönkre, naponta legfeljebb két
epizódot vetítettek. Az 1230-adik rész vetítésekor a nézők nagyon
elszomorodtak, mert a főszereplők összevesztek, de épp két évre
rá, 1992-ben, – mindenki nagy örömére –
kibékültek. Kár, hogy ez egyben az utolsó rész volt!
Hány
részből állt a sorozat?
Megoldás
59. Keress olyan hatjegyű számot,
ami köbszám, és a jegyeinek ciklikus átrendezéséből adódó hat
szám mindegyike osztható a szám köbgyökével!
Megoldás
60. Egy kocka lapjait 4-4
négyzetre osztottuk föl. Tekintsük azokat a kis
szakaszokat, amelyek a kocka lapjain található összesen 24
négyzet közül egyszerre kettőnek is oldalai. Ezek közül
26 piros. Bizonyítsd be, hogy van olyan zárt töröttvonal,
ami csupa piros szakaszból áll!
Megoldás
60. Nem nehéz megmutatni, hogy
2 osztható 21-vel,
3.4 osztható
22-nal,
4.5.6
osztható 23-nal.
Fogalmazd meg a fenti állítások közös
általánosítását, és bizonyítsd is be!
Megoldás
62. Egy füzetlap 33x41 kis
négyzetből áll. Be lehet-e írni a számokat 1-től 33 x 41 = 1353-ig a
négyzetekbe úgy, hogy minden 2x2-es négyzetben a számok összege
ugyan-annyi legyen?
Megoldás
63. A taxisok egyesülete
kirándulást szervezett egy iskola számára. Amikor az autós konvoj az
iskola elé érkezett, akkor minden mikrobuszba 12 diák, a Volgákba
pedig 7-7 diák szállt be. Később még három jármű érkezett, ami
csökkentette a zsúfoltságot. Az átülés után minden
mikrobuszban már csak 11-11, a Volgákban pedig 6-6 diák tartózkodott.
Meg lehet-e oldani néhány újabb Volga és mikrobusz
igénybevételével, hogy a személyautókban csak 5-5, a kisbuszokban
pedig 10-10 diák üljön?
Megoldás
64. Ketten a következő
játékot játsszák:
12 gyufa van az asztalon egy kupacban. A
játékosok felváltva lépnek, minden lépésben vagy elvesznek egy vagy
két gyufát a kupacból, vagy a már elvett gyufákból visszatesznek
egyet vagy kettőt a kupacba. Minden lépésük után a játékosok
felírják saját papírjukra a kupacban maradt gyufák számát. Az veszt,
aki már csak úgy tud lépni, hogy papírjára egy már ott levő számot
kelljen újra fölírnia.
Kinek van nyerő stratégiája?
És
ha 13 gyufából áll a kupac?
Megoldás
65. Leírtuk sorban egymás után a
pozitív négyzetszámokat:
149162536...
Melyik szám áll az 1993. helyen?
Megoldás
66. Egy pontosan járó
óra nagy és kismutatója végpontjának egymáshoz viszonyított sebessége
egy adott pillanatban 10 mm/s. Lehet-e egy másik pillanatban ez a
relatív sebesség 8 mm/s? És 12 mm/s?
Megoldás
67. A négyzethálós füzetben
adott három rácspont
A,
B és
C. Az
ABC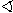
éppen 45
o-os és az
AB,
BC szakaszok
belsejében nincsenek rácspontok, csak a végpontok azok. Bizonyítsd
be, hogy az ABC háromszög derékszögű!
Megoldás
68. Bizonyítsd be, hogy
(n + 1)1993 + n1993
+ (n – 1)1993 – 3n
bármely
n természetes szám esetén osztható
10-zel.
Megoldás
69. Vettünk egy ötjegyű
számot. Számjegyeit leírtuk fordított sorrendben is, így kaptunk egy
másik ötjegyű számot. A két szám közül a nagyobbikból
kivontuk a kisebbiket, így kaptuk az
A számot. Ha megmondanám
neked
A utolsó három jegyét, ki tudnád-e találni
A-t?
Megoldás
70. Keresd meg a természetes
számokból álló összes olyan
A, B, C számhármast, amelyre
AB + BC + CA = 2(A + B
+ C)!
Megoldás
71. A könyvszekrény
egyik polcán áll Jules Verne összes műve nyolc kötetben.
Sajnos a kötetek összekeveredtek. Kihúzhatjuk, balról
jobbra számolva, a harmadik vagy a nyolcadik könyvet, és azt a
sor elejére tehetjük. Bizonyítsd be, hogy ilyen lépésekkel
elérhető, hogy a könyvek a helyes sorrendbe kerüljenek!
Megoldás
72. Melyik az a csupa különböző
számjegyből álló ötjegyű szám, amelyik egyenlő a számjegyeiből
alkotható összes háromjegyű szám összegével?
Megoldás
73. Az
M és
N
pontokat rendre az
ABC háromszög
AB,
BC
oldalain vettük föl. Bizonyítsd be, hogy ha
BNM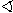 < ANM
< ANM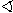
,
akkor
BMN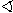
>
CMN
!
Megoldás
74. Andris bejelölte 1999.
évi naptárjába barátainak születésnapját. A következőket
vette észre ezzel kapcsolatban:
1. Semelyik két dátum sem egyezett meg teljesen.
2. Nem esett mindegyik ugyanabba a hónapba.
3. Nem esett mindegyik a hétnek ugyanazon napjára.
4. Nem esett mindegyik hónapjának ugyanannyiadik
napjára.
5. Bármelyik két születésnap vagy ugyanabban a
hónapban volt, vagy a hétnek ugyanazon napjára esett, vagy hónapjának
ugyanannyiadik napja volt.
Legfeljebb hány barátja lehet Andrisnak?
Megoldás
75. Ha a kockát
kiterítjük, 6 egybevágó négyzetet kapunk. össze lehet-e
állítani 5 egybevágó téglalapból egy kiterített paralelepipedont?
Megoldás