Az 1995. évi nyári tábor
feladatai
Egyéni verseny (Olimpia)
T. 156 Egy diáktalálkozón 19 tanuló vett részt. A
találkozót követő napokban elkezdtek egymással levelezni, mindegyikük 2
vagy 4 levelet adott fel. Lehetséges-e, hogy mindegyikük pontosan 3
levelet kapott?
Megoldás
T. 157 Az
a oldalú
ABCD négyzet
AB oldalára befelé állítottuk az
ABE szabályos háromszöget.
Határozd meg a
CDE háromszög körülírt körének
sugarát!
Megoldás
T. 158 Határozd meg azt a legkisebb 1995-tel osztható
természetes számot, amelynek bármely két másodszomszédos számjegye egyenlő
egymással.
Megoldás
T. 159 Mutasd meg, hogy az 1!ˇ2!ˇ3!ˇ...ˇ98!ˇ99!ˇ100!
szorzat 100 tényezője közül el lehet úgy hagyni egyet, hogy a maradék 99
tényező szorzata négyzetszám legyen!
Megoldás
T. 160 Az
ABC egyenlő szárú derékszögű
háromszög
AC átfogóján úgy vettük fel az
M és
K
pontokat, hogy
M az
A és
K közé essen és, hogy az
MBK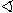
> 90º-os legyen. Bizonyítsd be, hogy
MK
2 =
AM 2 +
KC 2.
Megoldás
T. 161 Ki lehet-e jelölni a 13x13-as táblázatban
néhány mezőt úgy, hogy a táblázat minden mezője pontosan egy kijelölt
mezővel legyen oldalával határos?
Megoldás
T. 162 Határozd meg az
ABC háromszög szögeit,
ha tudjuk, hogy
AB =
BC és azt is, hogy az
AT
magasság fele olyan hosszú, mint az
AH
szögfelező!
Megoldás
Szakkörök közti
vetélkedők
1. változat
T. 163 Bizonyítsd be, hogy ha az
a,
b,
c egész számok olyanok, hogy az
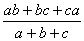
tört értéke is egész szám, akkor
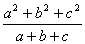
is egész!
Megoldás
T. 164 Színezd ki a 3x3-as táblázat mezőit minél több
színnel úgy, hogy bármely két használt színhez található legyen egy-egy
ilyen színű, oldalukkal szomszédos mező. (Az egyes mezőknek csak egyféle
színe lehet!)
Megoldás
T. 165 Kilenc szám van a táblán: egy háromszög három
magasságának, három súlyvonalának és három szögfelezőjének hossza.
Bizonyítsd be, hogy ha a kilenc szám között csak legfeljebb négy különböző
van, akkor a háromszög egyenlő szárú!
Megoldás
T. 166 Lehet-e 13 egymást követő természetes szám
négyzetösszege négyzetszám?
Megoldás
T. 167 A Bergengóc Országgyűlés 100 képviselője a
Parlament nagytermének 10 padsorában 10 oszlopban foglal helyet. A
küldötteknek mind különböző a fizetése. Minden képviselő megkérdezi
szomszédait (a maga mellett, előtt, mögött ülőket és az átlós szomszédait
is, összesen tehát legfeljebb 8-at), hogy mennyi a fizetésük. A küldöttek
meglehetősen irigyek: csak azok elégedettek a bérükkel, akiknek legfeljebb
egy olyan szomszédja van, aki többet keres náluk.
Legfeljebb hány olyan képviselő lehet a Parlamentben, aki meg van
elégedve a fizetésével?
Megoldás
T. 168 Az egyfordulós, körmérkőzéses röplabda
bajnokság végén kiderült, hogy a résztvevő csapatokat
k csoportba
lehet osztani úgy, hogy a csoportot alkotó csapatok győzelmeinek számát
összeadva minden csoport esetén ugyanazt az összeget kapjuk.
Határozd meg
k értékét, ha tudjuk, hogy az első csoport 1
csapatból, a második 2-ből, ... , a
k-adik
k csapatból
áll!
Megoldás
T. 169 Írj az azonos betűk helyére egyforma, a
különböző betűk helyére különböző számjegyeket úgy, hogy teljesüljön az
összeadás: SONK,A + SONK,A = MALAC.
Megoldás
2. változat
T. 170 Egy játék táblája 1995 mezőből áll, amelyek
körben helyezkednek el. Minden mezőbe egy-egy természetes szám van írva.
Az egyik mezőn egy bábú áll. Egy lépés- ben a bábút annyi mezővel
visszük arrébb az óra járásának irányában, amennyi a kiindulási
mezőre volt írva. Egyúttal az érkezési mezőre írt számot eggyel
megnöveljük. Így haladunk tovább. Igaz-e, hogy előbb vagy utóbb a bábú
bejárja a tábla összes mezőjét?
Megoldás
T. 171 Bizonyítsd be, hogy ha
xy +
z =
yz +
x =
zx +
y, akkor (
x - y)(
y -
z)(
z - x) = 0.
Megoldás
T. 172 Egy játék táblája
100 000 egymás mellé rajzolt négyzetből áll. A négyzetek kezdetben üresek.
Ketten játszanak, felváltva lépnek. Kezdő kiválaszt két tetszőleges üres
négyzetet és egy-egy "x”-et rajzol rájuk. Második akárhány, egymás
melletti "x”-et kiradírozhat (de üres négyzeten nem ugorhat át). Alább egy
játék első néhány lépése látható:
Kezdő nyer, ha
valamelyik lépése után 13 szomszédos négyzetben is "x” van. Tud-e nyerni
Kezdő, ha Második ügyesen játszik?
Megoldás
T. 173 Tizenkét ember ül
egy asztal körül: lovagok és lókötők. Így szólt mindegyikük:
mindenki – esetleg rajtam és
szomszédaimon kívül – lókötő.
Hány lovag ül az asztalnál, ha tudjuk, hogy a lókötők mindig hazudnak, a
lovagok pedig mindig igazat mondanak?
Megoldás
T. 174 Az
ABC háromszögben az
A
csúcsnál fekvő belső szög 60º-os, a
BM súlyvonal pedig egyenlő
hosszú a
CN magassággal. Határozd meg a háromszög többi szögét!
Megoldás
T. 175 Van-e olyan
természetes szám, amely éppen 1995-ször akkora, mint
prímosztóinak összege?
Megoldás
T. 176 Egy ötjegyű
számot, amely csupa különböző számjegyből áll, megszoroztunk néggyel. Így
egy olyan ötjegyű számot kaptunk, amelyet ugyanazok a számjegyek alkotnak,
de most épp fordított sorrendben. Melyik ez a szám?
Megoldás
T. 177 Fel lehet-e
osztani a négyzethálós papírra rajzolt 1995x1995-ös négyzetet a
négyzetháló vonalai mentén 10 000 olyan téglalapra, amelyeknek az átlói
mind egyenlő hosszúak?
Megoldás
3. változat
T. 178 Keress 6 olyan pontot a síkon, amelyek közül
bármely 5 letakarható két darab egységnyi átlójú négyzetlappal, de mind a
6 nem fedhető le 2 db egységnyi átmérőjű körlappal!
Megoldás
T. 179 Az
ABC háromszög
A-nál fekvő
belső szöge 30º, a
BM súlyvonal pedig egyenlő a
BC oldallal.
Határozd meg a háromszög belső szögeit!
Megoldás
T. 180 Egy hatjegyű szám első jegye 1-es. Ha ezt a
számjegyet áttesszük a szám végére, akkor a szám a háromszorosára
nő. Melyik ez a szám?
És ha nem tesszük föl, hogy a szám hatjegyű?
Megoldás
T. 181 Keresd meg az összes olyan
a, b, c
természetes számokból álló számhármast, amelyre
a+b+c prím és
(
a2+
b2+
c2) osztható
(
ab +
bc +
ca)-val!
Megoldás
T. 182 Egy
nx
n-es sakktábla (
n
³ 3) bal alsó sarkában áll
egy huszár. Tudjuk, hogy a legkisebb lépésszám, amivel a huszár átjuthat a
jobb fölső sarokba megegyezik a legkisebb lépésszámmal, amivel a jobb alsó
sarokba juthat. Mekkora lehet
n?
Megoldás
T. 183 Egy parasztnak volt egy kis csikója, egy
kancája és egy kecskéje. Volt neki ezeken kívül még egy kazalnyi szénája
és egy kamaszka szép lánya. A leányka kiszámolta, hogy a kazalnyi széna
elég a kecskének és a csikónak 1 hónapra, a csikónak és a kancának 3/4
hónapra vagy a kancának és a kecskének 1/3 hónapra. Papája szerint a leány
rosszul tanult az iskolában. Igaza volt-e?
Megoldás
T. 184 A táblán egy csupa 7-esből álló természetes
szám állt. Peti letörölte a szám utolsó jegyét, a kapott számot
megszorozta hárommal és a szorzathoz hozzáadta az előbb letörölt számot.
Mindezeket addig ismételgette, míg egy egyjegyű számot kapott. Mi
lehetett ez?
Megoldás
T. 185 15 lámpa egy körben helyezkedik el. Mindegyik
lámpa vagy ég vagy nem ég.
Egy lépésben megváltoztathatjuk három egymást követő lámpa állapotát:
az égőket leoltjuk, amelyik nem égett, azt fölkapcsoljuk. El
lehet-e érni, hogy minden lámpa ég- jen, ha kezdetben csak egy
égett?
Megoldás
T. 186 Az
ABC háromszögben
AB =
BC és a
B-ből induló magasság
hossza fele az
A-ból induló szögfelezőének. Határozd meg az
ABC háromszög szögeit!
Megoldás
T. 187 Az
ABC derékszögű háromszögben az
AC befogó hossza 3 egység, míg a
BC befogóé 4 egység
volt. Az
A pontot elmozdítottuk a
BC egyenessel
párhuzamosan. Ezután a
B pontot mozgattuk el az
AC
egyenessel párhuzamosan, végül a
C helyzetét változtattuk meg
AB-vel párhuzamosan. Így olyan háromszöghöz jutottunk, amelyben
B-nél lett derékszög, az
AB szakasz hossza pedig 1 egységnyi
lett. Milyen hosszú lett a
BC szakasz?
Megoldás
T. 188 Egy körön szeretnénk elhelyezni 8 számot úgy,
hogy mindegyik egyenlő legyen az óra járása szerint utána
következő három szám összegével. Hány megoldás van?
Megoldás
T. 189 Írd föl az 1, 1/2, 1/3, ... 1/10 számokat
valamilyen sorrendben és tegyél közéjük műveleti jeleket úgy, hogy 0-t
kapj eredményül!
Megoldás
T. 190 Föl lehet-e osztani egy négyzetet egy
ezerszögre és 199 ötszögre?
Megoldás
T. 191 Egy 5x5-ös táblázat mezőit négy színnel
színeztük ki úgy, hogy bármelyik 2x2-es részben mind a négy szín
előforduljon. Legfeljebb hányszor fordulhat elő egy szín az 5x5-ös
táblázatban?
Megoldás
T. 192 Hat focicsapat körmérkőzéses tornán vett
részt. Mindenki mindenkivel egyszer játszott. A bajnokság végén az egyes
csapatok 12, 10, 9, 8, 7 illetve 6 pontot gyűjtöttek össze. Hány pont járt
a győzelemért, ha döntetlenért 1, vereség esetén 0 pontot kapott minden
csapat?
Megoldás
T. 193 Adott három természetes szám, amelyek közül
bármelyik kettő összege prím. Bizonyítsd be, hogy az adott számok között
vannak egyenlők.
Megoldás
5. változat
T. 194 Az
A és
B természetes
számok közül az egyik jegyeinek összege 1993, a másik jegyeinek összege
pedig 1994. Lehetséges-e, hogy
A+
B jegyeinek összege 1995?
Megoldás
T. 195 Fel lehet-e osztani egy négyzetet
háromszögekre úgy, hogy mindegyik háromszög három máik háromszöggel legyen
határos (az oldala mentén)?
Megoldás
T. 196 A felsőosztályos fiútestvér így szólt
húgocskájához: "Hány napig voltál épp
harmad annyi éves, mint
én?”. "Három napig” -válaszolta húga. "És negyedannyi éves?”
- "4
napig. "No és hatodannyi éves?” Ezen a kishúg már elgondolkodott. Tudta,
hogy voltak ilyen napok, de hogy hány? Segíts neki válaszolni!
Megoldás
T. 197 Van-e két olyan konvex négyszög, amelyek
bármelyikének bármelyik oldala rajta van a másik négyszög valamelyik
oldalának felezőmerőlegesén?
Megoldás
T. 198 Be lehet-e helyettesíteni az 1, 2, 3, 4, 5
számokat az
a, b, c, d, e változók helyébe úgy, hogy teljesüljön az
(a+b)(b+c)(c+d)(d+e)(e+a)=(a+c)(c+e)(e+b)(b+d)(d+a)
összefüggés?
Megoldás
T. 199 Melyik az a legkisebb pozitív egész szám,
amely két kétjegyű egész szám hányadosának 100-szorosa?
Megoldás
T. 200 Ketten játszanak. A játékhoz szükség van 1800
színes korongra, 18 szín mindegyikéből 100-ra, továbbá egy 9×9-es táblára.
Kezdőnek csak az a dolga, hogy kiválasszon egy korongot és azt Másodiknak
adja. Második a kapott korongot a táblára helyezi. Ha öt ugyanolyan színű
korong egy sorban vagy egy oszlopban egymás mellé kerül, akkor leveszik
őket a tábláról és többé nem is kerülnek vissza a játékba. Ha Második a
kapott korongot már sehová se tudja letenni, akkor vesztett. Kezdő
pe- dig akkor veszít, ha már minden korongja elfogyott. Kinek van nyerő
stratégiája?
Megoldás
T. 201 Lehetséges-e, hogy egy háromszög egyik
csúcsához tartozó szögfelezője, egy másik csúcsához tartozó magasságvonala
és a harmadik csúcsból induló súlyvonala egy (nem nulla területű)
szabályos háromszöget határol?
Megoldás
6. változat
T. 202 Tíz nem feltétlenül különböző szám van a
táblán. Tudjuk, hogy bármelyik három számtani közepe is a táblán van.
Bizonyítsd be, hogy ez csak akkor lehetséges, ha ezek a számok mind
egyenlőek.
Megoldás
T. 203 Föl lehet-e írni az 1, 2, 3, ... 64 számokat a
sakktábla mezőire úgy, hogy semelyik két oldalával vagy csúcsával
határos mezőn álló két szám összege se legyen oszt- ható 4-gyel?
Megoldás
T. 204 Keresd meg az
ABCD négyzet belsejében
az összes olyan
P pontot, amelyre
PA + PC= PB + PD.
Megoldás
T. 205 Az
ABC háromszög
A csúcsánál tompaszög van és az
AB,
AC egyenesekre
A-ban állított merőlegesek az
BC oldalt három egyenlő részre
osztják. Határozd meg az
ABC háromszög szögeit.
Megoldás
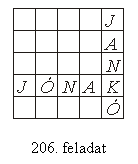
T. 206 Töltsd ki a megadott táblázat üres mezőit az
A, J,
K,
N,
Ó betűkkel úgy, hogy mindegyik
sorban, mindegyik oszlopban és mind a két átlóban mindegyik betű
előforduljon.
Megoldás
T. 207 Bizonyítsd be, hogy ha az 100...01 alakú
A szám osztható 19-cel, akkor 13-mal is osztható.
Megoldás
T. 208 Néhány ötven literes hordót teletöltöttek
kvásszal. Ha 40 literes hordókba töltötték volna az italt, akkor 5
hordóval többre lett volna szükség, de az egyik nem lett volna tele. Ha
viszont 70 literes hordókba töltötték volna, akkor 4 hordóval többre lett
volna szükség, de akkor is lett volna egy, amelyik nem megy tele. Hány
liter a kvász mennyisége?
Megoldás
T. 209 Ketten játszanak, felváltva húzzák be egy
szabályos 1995-szög egy-egy átlóját. Tilos olyan átlót behúzni, amely
metsz egy már korábban berajzoltat. Az
veszít, akinek a lépése után
létrejön egy olyan négyszög, amelynek egyik átlója sincs behúzva. Kinek
van nyerő stratégiája?
Megoldás
T. 210 Lehet-e egy kocka csúcsaihoz különböző
számokat írni úgy, hogy épp akkora
Legyen mindegyik szám, mint a kockán él mentén vele szomszédos másik
három szám összege?
Megoldás
T. 211 Egy téglalap alakú papírból két egybevágó kört
vágtunk ki. Melyik egyenes mentén lehet úgy szétvágni a papírt, hogy két
egyenlő területű részre essen szét?
Megoldás
T. 212 András 10
18-kor indult
A
helységből, és egyenletes sebességgel haladva 13
30-ra ért
B-be. Ugyanezen a napon 9
00-kor indult el Bence
B-ből és ugyanazon az úton, de ellenkező irányba tartva, mint
András, egyenletes sebességgel haladt, és 11
40-re ért
A-ba. Az utat egy folyó keresztezte. András és Bence egyszerre
értek a hídhoz, de András egy perccel később ért át rajta, mint Bence.
Mikor érték el a hidat?
Megoldás
T. 213 Egy 1995-oldalú zárt töröttvonal csúcsai
egyben egy szabályos 1995-szög csúcsai is. Bizonyítsd be, hogy a
töröttvonalnak van három egyenlő hosszú oldala.
Megoldás
T. 214 Lehetséges-e olyan társaság, amelyben
mindenkinek pontosan 6 barátja van, és bármely két embernek éppen 2
közös barátja van?
Megoldás
T. 215 Ketten játszanak egy "végtelen” négyzethálós
papíron: felváltva színezik be a négyzetek egy-egy oldalát. Nyolcféle
színt használhatnak. Kezdő arra törekszik, hogy létrejöjjön egy olyan zárt
töröttvonal, amelynek bármely két szomszédos oldala különböző színű. Meg
tudja-e ebben akadályozni Második?
Megoldás
T. 216 Jelölje
p(
n) az
n
természetes szám számjegyeinek szorzatát. Számold ki a
p(1000) + p(1001) + ? + p(2000) összeg
értékét!
Megoldás
T. 217 Egy konvex négyszög oldalait az óra járásának
megfelelő irányban 1:2 arányban osztottuk föl. Bizonyítsuk be, hogy ha az
osztópontok paralelogramma alkotnak, akkor az eredeti négyszög is
paralelogramma!
Megoldás
T. 218 Van-e két olyan természetes szám, amelyek
legkisebb közös többszöröse egyenlő az összegükkel?
Megoldás
T. 219 Adott az
ABC háromszög. Egy
AC-vel párhuzamos egyenes az
AB oldalt
P-ben, az
AM súlyvonalat
T-ben, a
BC oldalt
K-ban
metszi. Határozd meg az
AC oldal hosszát, ha tudjuk, hogy
PT
= 3,
TK = 5.
Megoldás
T. 220 Egy sakktáblán 8 dominót helyeztek el úgy,
hogy mindegyik pontosan két szomszédos mezőt fed. Bizonyítsd be, hogy a
sakktáblának van olyan 4 mezőből álló négyzetalakú része, amelyen nincs
dominó.
Megoldás
T. 221 Egy 7×7-es táblázat mezőibe a 0, 1, -1
számokat írták úgy, hogy minden 3×3-as négyzetben a számok összege 0.
Legfeljebb mekkora lehet a táblázatban található összes szám
összege?
Megoldás
T. 222 Bizonyítsd be, hogy 1994
2 +
1994
2 ×1995
2
+1995
2 négyzetszám!
Megoldás
T. 223
 Lehetséges-e olyan társaság,
amelyben mindenkinek pontosan 5 barátja van, és bármely két embernek
éppen 2 közös barátja van?
Lehetséges-e olyan társaság,
amelyben mindenkinek pontosan 5 barátja van, és bármely két embernek
éppen 2 közös barátja van?
Megoldás
T. 224 Van-e olyan konvex hétszög, amelyben mindegyik
átló merőleges valamelyik másik átlóra?
Megoldás
T. 225 Téglalapokra szeretnénk szétvágni az ábrán
látható rostélyt. Legkevesebb hány téglalap keletkezik, ha csak a
négyzetháló vonalai mentén vághatunk?
Megoldás
![]()


 Lehetséges-e olyan társaság,
amelyben mindenkinek pontosan 5 barátja van, és bármely két embernek
éppen 2 közös barátja van?
Lehetséges-e olyan társaság,
amelyben mindenkinek pontosan 5 barátja van, és bármely két embernek
éppen 2 közös barátja van?