Megoldások
Az 1995. évi nyári tábor feladatai

Tehát a keresett számnak legalább hatjegyűnek kell lennie. Ekkor a
keresett számot így is felírhatjuk:
![]() . A
10101 nem osztható 19-cel, de a számnak osztódnia kell vele, ezért
. A
10101 nem osztható 19-cel, de a számnak osztódnia kell vele, ezért
![]() -nek 19
többszörösének kell lennie. A 19 kétjegyű többszörösei: 19, 38, 57, 76,
95. De az utolsó számjegy, tehát b csak 0 vagy 5 lehet, ezért csak
a 0-ra vagy az 5-re végződő kétjegyű számok jók. Ezek között csak a 95
ilyen. Ekkor a hatjegyű szám: 959595. Ez osztható 1995-tel, és minden
másodszomszédos számjegye egyenlő, ezért ez egy jó megoldás. Mivel több
hatjegyű jó megoldás nincs, ezért ez a legkisebb jó megoldás.
A legkisebb ilyen természetes szám a 959595.
-nek 19
többszörösének kell lennie. A 19 kétjegyű többszörösei: 19, 38, 57, 76,
95. De az utolsó számjegy, tehát b csak 0 vagy 5 lehet, ezért csak
a 0-ra vagy az 5-re végződő kétjegyű számok jók. Ezek között csak a 95
ilyen. Ekkor a hatjegyű szám: 959595. Ez osztható 1995-tel, és minden
másodszomszédos számjegye egyenlő, ezért ez egy jó megoldás. Mivel több
hatjegyű jó megoldás nincs, ezért ez a legkisebb jó megoldás.
A legkisebb ilyen természetes szám a 959595.
Ha ebből a szorzatból az 50!-t elhagyjuk, akkor egy olyan szorzatot kapunk, amelynek minden tényezője négyzetszám, tehát a szorzat is négyzetszám. Tehát az eredeti szorzatból az 50!-t elhagyva négyzetszámot kapunk.
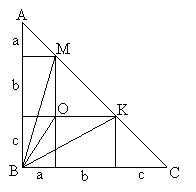
II. megoldás:

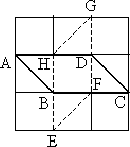
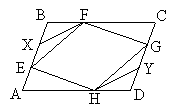
BM-re nézve AM szakasz tükörképe DM szakasz, ezért AM =
DM, tehát AMD háromszög egyenlő szárú, DAM![]() =
ADM
=
ADM![]() =
=
![]() . BK-ra nézve CK szakasz tükörképe DK szakasz, ezért
CK = DK, tehát CDK háromszög egyenlő szárú, DCK
. BK-ra nézve CK szakasz tükörképe DK szakasz, ezért
CK = DK, tehát CDK háromszög egyenlő szárú, DCK![]() =
CDK
=
CDK![]() =
=
![]() . BEDF négyszög belső szögeinek összege 360˚ , ezért
EDF
. BEDF négyszög belső szögeinek összege 360˚ , ezért
EDF![]() + 90° + 90° + 45° = 360°, tehát EDF
+ 90° + 90° + 45° = 360°, tehát EDF![]() =
ADC
=
ADC![]() = 135°. ACD háromszög szögeinek összege 180˚ , ezért
= 135°. ACD háromszög szögeinek összege 180˚ , ezért
![]() +
+
![]() + 135°=180°,
tehát
+ 135°=180°,
tehát
![]() +
+
![]() = 45°.
MDK
= 45°.
MDK![]() = 135° - (
= 135° - (![]() +
+
![]() ) = 135° - 45°
= 90°, ezért MDK háromszög derékszögű. A Pithagorasz tétel szerint
DM2 + DK2 = MK2, de
AM = DM és KC = DK, ezért
AM2 + KC2 = MK2, és
ezt kellett bebizonyítani.
) = 135° - 45°
= 90°, ezért MDK háromszög derékszögű. A Pithagorasz tétel szerint
DM2 + DK2 = MK2, de
AM = DM és KC = DK, ezért
AM2 + KC2 = MK2, és
ezt kellett bebizonyítani.
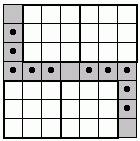
Ha az (a - 1; b) és (a; b - 1) mezők nem kijelöltek, akkor (a; b) mező másik két szomszédja között van kijelölt. Ezek az (a + 1; b + 1) mezőnek is szomszédjai, így ennek másik két szomszédja nem kijelölt, tehát (a + 1; b + 2) és (a + 2; b + 1) mezők nem kijelöltek.
(2; 3) és a (3; 2) nem kijelölt, ezért (4; 5) és (5; 4), (6; 7) és (7;
6), (8; 9) és (9; 8),
(10; 11) és (11; 10), (12; 13) és (13; 12) mezők
sem kijelöltek. Az utolsó kettő a jobb alsó mező két szomszédja. Tehát a
jobb alsó mezőnek nincs kijelölt szomszédja, ezért nem lehet így
kijelölni néhány mezőt.
Általánosítás: Ugyanaz a kérdés n×n-es táblázat esetén. Ha n páratlan:
Ha n = 1, akkor nincs megoldás. Ha n > 1, akkor pedig már ugyanúgy gondolkodhatunk, mint az előző megoldásban, tehát a (2; 3) és (3; 2), (4; 5) és (5; 4), ..., (n - 1; n) és (n; n - 1) mezők nem lehetnek kijelöltek. Így az (n; n) mezőnek nincs kijelölt szomszédja, ezért itt sincs megoldás. Tehát ha n páratlan, akkor nincs megoldás.
Ha n páros: ha n értéke 2, 4, vagy 6, akkor van megoldás. Ha n > 6:
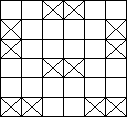
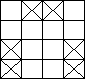
![]()
Tegyük fel, hogy n - 4-re van megoldás. Ekkor n-re is
van. Ebben a megoldásban a (3; 3),
(3; n - 2), (n - 2;
3), (n - 2; n - 2) csúcsokkal rendelkező,
(n-4)×(n-4)-es négyzet tartalma megegyezik az előző
megoldáséval. E négyzetet kívülről legalább 1 pontban határoló mezők
nincsenek kijelölve. Az n×n-es négyzet szélén lévő mezők
közt a bal felső saroktól kezdve az óramutató járásával megegyező irányban
felváltva van 2 kijelölt és 2 nem kijelölt mező. Tehát a bal felső sarok
kijelölt. Egy kis gondolkodással rájöhetünk, hogyha mindig az előzőleg
megkapott megoldást használjuk, akkor ez egy jó megoldást fog
eredményezni. Így ha n - 4-re van megoldás, akkor n-re is.
Legyen n = 8. Ekkor n - 4-re van megoldás, ezért n-re
is lesz. Növeljük n-t mindig 4-gyel. Ekkor n-re mindig lesz
megoldás, tehát a 4-gyel oszthatókra van megoldás. Most legyen n =
10. Ekkor n - 4-re van megoldás, ezért n-re is lesz.
Növeljük n-t mindig 4-gyel. Ekkor n-re mindig lesz megoldás,
tehát a 4-gyel osztva maradékul 2-t adóknál van megoldás. Tehát ha
n páros, akkor van megoldás.
Páratlan oldalszám esetén nincs megoldás, páros esetén pedig mindig van.
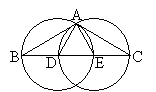
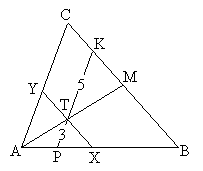
Tegyük fel, hogy minden magasság különböző. Legyenek a háromszög
csúcsai megint A, B, C, és a leghosszabb magasság AE.
Legyen az A-ból induló szögfelező AF, és az A-ból induló
súlyvonal AG. Ha AE = AF, akkor E és F pontok
megegyeznek, mert BC egyenes A-tól való távolsága AE, ezért BC
egyenesen lévő E-től különböző pontok A-tól való távolsága
nagyobb AE-nél. BAE![]() =
CAE
=
CAE![]() , AEB
, AEB![]() =
AEC
=
AEC![]() = 90°, ABC
= 90°, ABC![]() =
180° - BAE
=
180° - BAE![]() -
AEB
-
AEB![]() , ACB
, ACB![]() =
180° - CAE
=
180° - CAE![]() -
AEC
-
AEC![]() , ezért ABC
, ezért ABC![]() =
ACB
=
ACB![]() , tehát ha AE = AF, akkor ABC
háromszög egyenlőszárú. Ha AE = AG, akkor E és
G pontok megegyeznek. ABE
, tehát ha AE = AF, akkor ABC
háromszög egyenlőszárú. Ha AE = AG, akkor E és
G pontok megegyeznek. ABE![]()
![]() ABF
ABF![]() , mert
AE közös, BE = CE, és a közrezárt szögeik is egyenlők:
AEB
, mert
AE közös, BE = CE, és a közrezárt szögeik is egyenlők:
AEB
![]() =
AEC
=
AEC![]() . Ezért AB = AC, tehát ABC háromszög
egyenlőszárú. Ha AE
. Ezért AB = AC, tehát ABC háromszög
egyenlőszárú. Ha AE![]() AF, és AE
AF, és AE![]() AG, akkor AF > AE és AG >
AE. Ekkor AF és AG minden magasságnál nagyobbak. Ha AF
AG, akkor AF > AE és AG >
AE. Ekkor AF és AG minden magasságnál nagyobbak. Ha AF![]() AG, akkor már 5 különböző érték lenne, ezért AF
= AG. Tükrözzük A-t F-re. Legyen a tükörképe
A'. Legyen BAC
AG, akkor már 5 különböző érték lenne, ezért AF
= AG. Tükrözzük A-t F-re. Legyen a tükörképe
A'. Legyen BAC![]() =
2
=
2![]() . Ekkor BAF
. Ekkor BAF![]() =
CAF
=
CAF![]() =
=
![]() , így
BA'F
, így
BA'F![]() = CA'F
= CA'F![]() =
=
![]() , ezért AA'B és AA'C háromszögekben AA' közös,
és a két hozzá tartozó szög egyenlő, tehát AA'B
, ezért AA'B és AA'C háromszögekben AA' közös,
és a két hozzá tartozó szög egyenlő, tehát AA'B![]()
![]() AA'C
AA'C
![]() AB = AC, ezért ABC háromszög egyenlőszárú.
Tehát a háromszög minden esetben egyenlőszárú.
AB = AC, ezért ABC háromszög egyenlőszárú.
Tehát a háromszög minden esetben egyenlőszárú.
|
101 |
102 |
103 |
104 |
105 |
106 |
107 |
108 |
109 |
110 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
111 |
112 |
113 |
114 |
115 |
116 |
117 |
118 |
119 |
120 |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
121 |
122 |
123 |
124 |
125 |
126 |
127 |
128 |
129 |
130 |
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
131 |
132 |
133 |
134 |
135 |
136 |
137 |
138 |
139 |
140 |
|
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
141 |
142 |
143 |
144 |
145 |
146 |
147 |
148 |
149 |
150 |
|
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
Ha x - z vagy y - z értéke 0, akkor (x-y)(y-z)(z-x) = 0 teljesül. Ha egyik értéke sem 0, akkor x - 1 = 0 és y - 1 = 0, tehát x = y = 1, vagyis x - y = 0. Ekkor pedig ( x-y)(y-z)(z-x) = 0 ismét teljesül. Tehát ez az egyenlet minden esetben teljesül.
A: 0; 0 B: 1; 0 C: 1; 1 D: 0; 1 E: 0,4; 0,5 F: 0,5; 0,6.
Vegyünk sorba minden esetet a szerint, hogy két négyzettel melyik pontot nem fedjük le (és melyik 5-öt fedjük le). A két négyzetet a csúcsai koordinátáival adjuk meg.
|
1. négyzet |
2. négyzet | |||||||||||
|
A |
0; 1 -
|
|
|
0; 1 |
1; 0 |
1,5; 0,5 |
1; 1 |
0,5; 0,5 | ||||
|
B |
0; 0 |
0,5; 0,5 |
0; 1 |
-0,5; 0,5 |
0,5; 0,5 |
1; 1 |
0,5; 1,5 |
0; 1 | ||||
|
C |
1 -
|
1; 0 |
1;
|
1 -
|
0; 0 |
0,5; 0,5 |
0; 1 |
-0,5; 0,5 | ||||
|
D |
1 -
|
1; 1 -
|
1; 1 |
1 -
|
0,5; -0,5 |
1; 0 |
0,5; 0,5 |
0; 0 | ||||
|
E |
0,5; 0,5 |
1; 1 |
0,5; 1,5 |
0; 1 |
0,5; -0,5 |
1; 0 |
0,5; 0,5 |
0; 0 | ||||
|
F |
0; 0 |
0,5; 0,5 |
0; 1 |
-0,5; 0,5 |
1; 0 |
1,5; 0,5 |
1; 1 |
0,5; 0,5 | ||||
Ha nincs az a, b, c számok között 0:
(a+b+c)2 osztói: 1, a + b +
c, (a+b+c)2. De 1 < ab +
bc + ca < (a+b+c)2, ezért
ab + bc + ca = a + b + c
![]() (b-1)a + (c-1)b +
(a-1)c = 0. a, b, c pozitív, ezért az
utolsó egyenlet bal oldalán lévő összeg minden tagja természetes szám,
tehát 0. De a, b, c nem 0, ezért a - 1 =
b - 1 = c - 1 = 0
(b-1)a + (c-1)b +
(a-1)c = 0. a, b, c pozitív, ezért az
utolsó egyenlet bal oldalán lévő összeg minden tagja természetes szám,
tehát 0. De a, b, c nem 0, ezért a - 1 =
b - 1 = c - 1 = 0
![]() a = b = c = 1. Ekkor a + b + c =
3, prím, ab + ac + bc = 3, a2 +
b2 + c2 = 3, és 3 osztható 3-mal.
Tehát ez is egy megoldás.
a = b = c = 1. Ekkor a + b + c =
3, prím, ab + ac + bc = 3, a2 +
b2 + c2 = 3, és 3 osztható 3-mal.
Tehát ez is egy megoldás.
Tehát a jó számhármasok: 0, 1, 1 és 1, 1, 1.
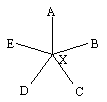
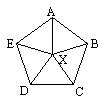
Tehát ABC![]() belső szögei 36˚ , 36˚ , 108˚ .
belső szögei 36˚ , 36˚ , 108˚ .
| 1 | 2 | 1 | 2 | 1 |
| 3 | 4 | 3 | 4 | 3 |
| 1 | 2 | 1 | 2 | 1 |
| 3 | 4 | 3 | 4 | 3 |
| 1 | 2 | 1 | 2 | 1 |
|
A |
B |
C |
D |
E |
F | |
|
A |
||||||
|
B |
+ |
|||||
|
C |
+ |
+ |
||||
|
D |
+ |
+ |
+ |
|||
|
E |
- |
0 |
0 |
+ |
||
|
F |
- |
0 |
+ |
+ |
0 |
Összesen
![]() =
15 mérkőzést játszottak. A döntetleneken összesen 2, más esetben összesen
x pontot kapott a két csapat. Ezért a bajnokság alatt kapott pontok
száma:
=
15 mérkőzést játszottak. A döntetleneken összesen 2, más esetben összesen
x pontot kapott a két csapat. Ezért a bajnokság alatt kapott pontok
száma:
De x > 2, ezért 2 - x < 0
![]() n(2-x)
n(2-x)
![]() 0
0
![]() 15x + n(2-x) = 52
15x + n(2-x) = 52
![]() 15x
15x
![]() 3
3![]()
![]() x. Ha valaki egyik mérkőzésen sem nyert volna, akkor
legfeljebb 5 pontja lehetne. Mindenkinek több van ennél, ezért mindenki
megnyert legalább 1 mérkőzést. Ha az utolsó csapat több mint két mérkőzést
megnyert volna, akkor 6-nál több pontja lenne, tehát pontosan 1 mérkőzést
nyert meg. Ha y a döntetleneinek a száma, akkor végül a pontszáma:
6 = x + y. Mivel y egész szám, ezért x is
egész. 3 < x
x. Ha valaki egyik mérkőzésen sem nyert volna, akkor
legfeljebb 5 pontja lehetne. Mindenkinek több van ennél, ezért mindenki
megnyert legalább 1 mérkőzést. Ha az utolsó csapat több mint két mérkőzést
megnyert volna, akkor 6-nál több pontja lenne, tehát pontosan 1 mérkőzést
nyert meg. Ha y a döntetleneinek a száma, akkor végül a pontszáma:
6 = x + y. Mivel y egész szám, ezért x is
egész. 3 < x
![]() 6,
ezért x csak 4, 5, 6 lehet. Ezeket az értékeket az (I.)-be
behelyettesítve ezeket kapjuk:
6,
ezért x csak 4, 5, 6 lehet. Ezeket az értékeket az (I.)-be
behelyettesítve ezeket kapjuk:
x = 4
![]() n =
n =
![]() = 4 ; x = 5
= 4 ; x = 5
![]() n =
n =
![]() = 7
= 7![]() x = 6
x = 6
![]() n =
n =
![]() = 9
= 9![]()
A
három eredmény közül csak a 4 egész, és n egész, ezért ez az
egyetlen lehetséges megoldás. Ekkor x = 4. Ezzel az értékkel meg is
valósítható a feladat, itt egy példa erre. Legyen a hat játékos A,
B, C, D, E, F. A + azt jelzi, hogy az
oszlophoz tartozó játékos nyert, a - azt, hogy ő vesztett, a 0 azt, hogy
döntetlen lett a mérkőzés végeredménye. A példában A, B,
C, D, E, F végső pontszámai rendre 12, 10, 9,
8, 7, 6, tehát ez egy jó megvalósítás.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
1. |
Fiú |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
10 |
|
Lány |
0 |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
|
2. |
Fiú |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
10 |
10 |
11 |
11 |
12 |
12 |
13 |
13 |
14 |
14 |
15 |
|
Lány |
0 |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
|
3. |
Fiú |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
10 |
10 |
11 |
11 |
12 |
12 |
13 |
13 |
14 |
|
Lány |
0 |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
|
4. |
Fiú |
10 |
11 |
11 |
12 |
12 |
13 |
13 |
14 |
14 |
15 |
15 |
16 |
16 |
17 |
17 |
18 |
18 |
19 |
19 |
20 |
|
Lány |
0 |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
|
5. |
Fiú |
9 |
10 |
10 |
11 |
11 |
12 |
12 |
13 |
13 |
14 |
14 |
15 |
15 |
16 |
16 |
17 |
17 |
18 |
18 |
19 |
|
Lány |
0 |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
|
6. |
Fiú |
15 |
16 |
16 |
17 |
17 |
18 |
18 |
19 |
19 |
20 |
20 |
21 |
21 |
22 |
22 |
23 |
23 |
24 |
24 |
25 |
|
Lány |
0 |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
|
7. |
Fiú |
14 |
15 |
15 |
16 |
16 |
17 |
17 |
18 |
18 |
19 |
19 |
20 |
20 |
21 |
21 |
22 |
22 |
23 |
23 |
24 |
|
Lány |
0 |
0 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
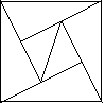
|
AB |
BC |
CD |
DA |
EF |
FG |
GH |
HE |
|
EF |
HE |
GH |
FG |
CD |
BC |
AB |
AD |
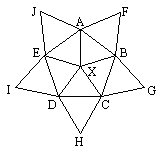
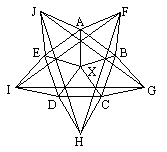
(a+b)(b+c)(c+d)(d+e)(e+a)(a+c)(c+e)(e+b)(b+d)(d+a)
Ebben az a, b, c, d, e számokból
álló kéttagú összegek mindegyike szerepel, ezért ugyanezt a szorzatot
kapjuk, ha az a, b, c, d, e
ismeretlenek közül bárhányat felcserélünk egymással. Így bárhogyan
helyettesítjük is be a számokat, a szorzat nem változik. Tehát elég egy
behelyettesítést megnézni:
(1+2)(2+3)(3+4)(4+5)(5+1)(1+3)(3+5)(5+2)(2+4)(4+1) = 38102400
De ez nem négyzetszám. Ellentmondásra jutottunk, tehát nem lehet ezt a
behelyettesítést elvégezni.
Ha
![]() . 100 = 15:
. 100 = 15:
![]() =
=
![]() =
=
![]() ,
tehát a tört a következők között van
,
tehát a tört a következők között van
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
...Ezek közül csak a
,
...Ezek közül csak a
![]() -ban kétjegyű a számláló és a nevező is. Tehát 15 csak a
-ban kétjegyű a számláló és a nevező is. Tehát 15 csak a
![]() -nál lehetséges.
-nál lehetséges.
Ha
![]() . 100 < 15:
. 100 < 15:
![]() . 100 lehetséges értékei: 14, 13, 12, 11. Mivel a
. 100 lehetséges értékei: 14, 13, 12, 11. Mivel a
![]() 10 és b < 100, ezért
10 és b < 100, ezért
![]() >
>
![]() , tehát
, tehát
![]() . 100 > 10. A felsorolt esetekben
. 100 > 10. A felsorolt esetekben
![]() értéke rendre
értéke rendre
![]() =
=
![]() ,
,
![]() ,
,
![]() =
=
![]() ,
,
![]() . Ezek a törtek már tovább nem egyszerűsíthetők, ezért
. Ezek a törtek már tovább nem egyszerűsíthetők, ezért
![]() lehetséges formái:
lehetséges formái:
E törtek közül egyiknek sem kétjegyű a számlálója és a nevezője is.
Tehát nincs olyan
![]() ,
amelyre
,
amelyre
![]() . 100 < 15.
. 100 < 15.
Ez a legkisebb egész szám a 15, és ez csak a
![]() . 100 = 15-re teljesül.
. 100 = 15-re teljesül.
Jelöljük a 18 színt a legkisebb 18 pozitív egésszel. Számozzuk meg a tábla minden sorának bal és jobb oldalát. Ez 18 szám, legyenek ezek a legkisebb pozitív egészek. Ezután a Második mindig ahhoz a széléhez teszi a korongot a táblának, ahol a korong színének megfelelő szám áll. Ha abban a sorban már van valahány ugyanilyen színű korong, akkor azok mellé teszi. Így mindig tud lépni Második, mert ha nem tudna, akkor lenne olyan sor, amely már megtelt. De egy sorban csak két szín van, ezért valamelyik színű korongból legalább 5-nek kell lennie. Ezek egymás mellett vannak, ekkor azonban már elvették volna őket a tábláról. Ellentmondásra jutottunk, ezért Második sosem fog veszteni. De Második minden lépésével eggyel csökken a korongok száma, ezért az 1800 korong véges időn belül elfogy, és ekkor Kezdő veszít, és Második nyer.
Csak akkor fordul elő egyenlőség, ha ai-1 =
ai = ai+1. Ekkor igaz, hogy a középső
szám megegyezik a számtani közepükkel. Ha az egyenlőség nem teljesül,
akkor csak a középső szám értéke lehet a számtani közép. Tehát három
szomszédos szám számtani közepe mindig a középső szám. Ebből következik,
hogy bármelyik két szomszédos szám különbsége ugyanannyi, legyen ez
x. Ekkor az első, a második és a negyedik szám rendre
a1, a1 + x,
a1 + 3x, így számtani közepük:
![]() =
a1 +
=
a1 +
![]() x. Ha x pozitív, akkor ez nagyobb, mint a
második, de kisebb, mint a harmadik szám, ezért ez nem lehetséges. Ha
x = 0, akkor minden szám egyenlő, és ekkor bármely három szám
számtani közepe a számok között van. Tehát ez csak akkor lehetséges, ha
minden szám egyenlő.
x. Ha x pozitív, akkor ez nagyobb, mint a
második, de kisebb, mint a harmadik szám, ezért ez nem lehetséges. Ha
x = 0, akkor minden szám egyenlő, és ekkor bármely három szám
számtani közepe a számok között van. Tehát ez csak akkor lehetséges, ha
minden szám egyenlő.
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
|
1 |
5 |
9 |
13 |
17 |
21 |
25 |
29 |
|
18 |
20 |
22 |
24 |
26 |
28 |
30 |
32 |
|
3 |
7 |
11 |
15 |
19 |
23 |
27 |
31 |
|
34 |
36 |
38 |
40 |
42 |
44 |
46 |
48 |
|
33 |
37 |
41 |
45 |
49 |
53 |
57 |
61 |
|
50 |
52 |
54 |
56 |
58 |
60 |
62 |
64 |
|
35 |
39 |
43 |
47 |
51 |
55 |
59 |
63 |
Ez csak úgy lehetséges, ha b2 = d2
![]() b = d vagy ha a2 -
c2 = 0
b = d vagy ha a2 -
c2 = 0
![]() a2 = c2
a2 = c2
![]() a = c. Mindkét esetben P az egyik szakasz
felezőpontja, ezért az eredeti két szakasz egyikén rajta van. Tehát a
keresett ponthalmaz a négyzet szemközti oldalainak felezőpontjait
összekötő szakaszok.
a = c. Mindkét esetben P az egyik szakasz
felezőpontja, ezért az eredeti két szakasz egyikén rajta van. Tehát a
keresett ponthalmaz a négyzet szemközti oldalainak felezőpontjait
összekötő szakaszok.
|
2 |
7 |
8 |
9 |
0 |
|
4 |
2 |
4 |
3 |
0 |
|
5 |
6 |
1 |
6 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
3 |
7 |
8 |
9 |
0 |
|
N |
K |
A |
Ó |
J |
|
K |
J |
Ó |
N |
A |
|
Ó |
A |
K |
J |
N |
|
J |
Ó |
N |
A |
K |
|
A |
N |
J |
K |
Ó |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
1 |
10 |
5 |
12 |
6 |
3 |
11 |
15 |
17 |
18 |
9 |
14 |
7 |
13 |
16 |
8 |
4 |
2 |
1 |
|
1 |
10 |
9 |
12 |
3 |
4 |
1 |
10 |
9 |
12 |
3 |
4 |
1 |
10 |
9 |
12 |
3 |
4 |
1 |
(I.) 40(x+5) > 50x > 40(x+4)
(II.) 70(x-4) > 50x > 70(x-5)
I.-ből: 40x + 200 > 50x > 40x + 160 200 > 10x > 160 20 > x > 16
II.-ból: 70x - 280 > 50x > 70x - 350 350 > 20x > 280 17, 5 > x > 14
Mivel x egész, ezért x már csak 17 lehet. Ekkor teljesül az utolsó két egyenlőtlenség, és mivel ekvivalens átalakításokat végeztünk, az eredeti feltételek is teljesülnek. Tehát a kvász mennyisége 50 . 17 = 850 liter.
5-szög: A kezdő bárhogy is lép, mindig kialakul egy négyszög, aminek nincs egy átlója sem, ezért a második nyer.
6-szög: A kezdő csak akkor nem veszít az első lépés után azonnal, ha egy 3-szögre és egy 5-szögre bontja a hatszöget. Ekkor a háromszögben már nem lehet átlókat behúzni, ezért a probléma visszavezetődött 5-szögre, ahol a második nyer, tehát most a kezdő nyer.
Megmutatjuk, hogy páratlan élszám esetén mindig a másodiknak, páros esetén mindig a kezdőnek van nyerő stratégiája. Tegyük fel, hogy n-nél kisebb élszámokra ez igaz. Ha n páros, akkor a kezdő tud nyerni, méghozzá ha egy háromszögre és egy n - 1 szögre bontja. Ha n páratlan, akkor a második tud nyerni. Az első lépése után a második kiválasztja a most behúzott átló egyik csúcsát. Ez a csúcs és az ettől legtávolabbi oldal középpontját összekötő egyenesre tükrözi a kezdő lépését. Így három sokszög alakul ki: a középső, amely páratlan oldalú, és két egybevágó szélső. Nem alakulhatott ki négyszög, mert az csak az egyik szélső sokszög lehetne, de ezek közül az egyiket még a kezdő hozta létre. Ezután, ha a kezdő az egyik szélső sokszögben lép, akkor a második a másik sokszögben a lépés tükörképét hajtja végre. Ha a kezdő a középső sokszögben lép, akkor a második úgy játszik, mintha csak ez a sokszög lenne. Ekkor a második tud nyerni, hiszen a középső sokszög páratlan oldalú, és n-nél kevesebb szögű. Így a második mindig tud lépni, és a játék valamikor véget ér, hiszen csak véges sok átló van, ezért a kezdő veszít, és a második nyer.
Az 1995 páratlan, ezért a másodiknak van nyerő stratégiája.
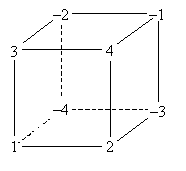
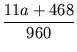 =
=
Tehát András elindulásától kezdve 42 perc múlva érték el a hidat, vagyis 11 órakor.
A p(1000) + p(1001) +...+ p(2000) összeg pontos értéke 453.

 |
| |||||||||||||||||||||||||||||||||||||||||||||||||
|
1. ábra |
2. ábra |
Az x = 1994 eset éppen a feladat állítása, mivel ekkor
Tehát a feladatban szereplő kifejezés négyzetszám.
 |
 |
 |
 |
|
1. ábra |
2. ábra |
3. ábra |
4. ábra |
 |
|
|
1. ábra |
2. ábra |