Az 1994/95. tanév
96. Egy sorozat első eleme 439, és
a sorozat következő tagját mindig úgy kapjuk, hogy az első tag
számjegyeinek összegét megszorozzuk 13-mal.
Határozd meg a sorozat 99. elemét!
Megoldás
97. Keresd meg az
összes olyan természetes számot, amelyben a jegyek szorzata 885
és 895 közé esik!
Megoldás
98. 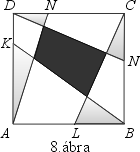
Az
a oldalú négyzetet az
AN,
BK,
CL,
DM
egyenesekkel részekre bontottuk (lásd a 8. ábrát!). Bizonyítsd be,
hogy ha a sötét négyszög területe megegyezik a
halványabban satírozott háromszögek területének összegével,
akkor
AM + BN + CK + DL = 2
a!
Megoldás
99. Az
A,
B,
C
egész számokra fennáll az alábbi összefüggés:
A.(A + B) = B.(B
+ C) = C.(C + A).
Bizonyítsd be, hogy
A =
B =
C!
Megoldás
100. Egy berendezés 100
világító gombból áll. A gombok 10 sorban és 10 oszlopban helyezkednek
el. Egy gomb megnyomásakor az ugyanabban a sorban illetve oszlopban
elhelyezkedő gombok egyszerre váltanak: az addig világítóak
kialszanak, a kikapcsoltak meggyulladnak. Legalább hány gombot kell
megnyomni ahhoz, hogy az összes gomb kialudjék, ha eredetileg
mind világított?
Megoldás
101. Keresd meg az összes
olyan természetes számot, amit nem lehet előállítani néhány (legalább
kettő) egymást követ? természetes szám összegeként!
Megoldás
102. Az
ABCD konvex
négyszög olyan, hogy a
DAC és
DBC szögek
szögfelezői a
CD oldalon metszik egymást. Bizonyítsd be,
hogy az
ADB és az
ACB szögek szögfelezőinek
metszéspontja az
AB oldalra esik!
Megoldás
103. Palindromnak nevezzük
azokat a szavakat, amelyeket hátulról is kiolvashatjuk, mert ugyanazt
kapjuk, mintha elölről olvasnánk. Palindrom szavak például a
SARAS vagy a MEREM.
Valaki fölírt a táblára egy csupa
A-ból
és
B-ből álló 1995 betűs sorozatot. Bizonyítsd be, hogy ezt a
sorozatot biztosan föl lehet bontani legfeljebb 800 olyan
rövidebb sorozatra, “szóra”, amelyek mindegyike
palindrom! (Pld. ABAAAB egy felbontása: [
ABA][
AA][
B].)
Megoldás
104. Járd be a
királlyal a sakktáblát úgy, hogy minden mezőre pontosan egyszer lépj,
és közben váltogasd az átlós és nem átlós lépéseket!
Meg tudod-e ugyanezt tenni 9x9-es táblán?
Megoldás
105. 6 egyformának
látszó pénzérménk van, amelyek közül azonban néhány hamis,
könnyebb az igazinál. Hogyan lehet egy kétkarú mérleg
segítségével, legfeljebb négy méréssel, segédsúlyok használata nélkül
kiválasztani az összes hamis érmét?
Megoldás
106. Keresd meg az összes
olyan természetes számot, amelyik egyenlő valamely két különböző
osztója összegének kétszeresével!
Megoldás
107. Egy nyolcfős baráti társaság
hétszer jött össze beszélgetni az Artúr sörözőben.
Mindig a kerek asztalhoz ültek, és az utolsó alkalommal
megállapították, hogy közülük bármelyik két ember
pontosan kétszer ült egymás mellett.
Lehetséges-e ez?
Megoldás
108. Adott a síkon
néhány, de legalább öt kör. Tudjuk, hogy közülük
bármelyik háromnak van közös pontja. Bizonyítsd be, hogy az
összes körnek is van egy közös pontja!
Megoldás
109. Bizonyítsd be, hogy
1991
.1993
.1995
.1997 + 16
négyzetszám!
Megoldás
110. 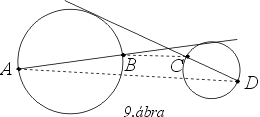
Adott a síkon két kör, az egyiken az
A és
B, a
másikon a
C és
D pontok úgy, hogy az
AB egyenes
átmegy az első kör középpontján és érinti a másikat, míg a
CD egyenes átmegy a másik kör középpontján és érinti
az elsőt (9. ábra).
Bizonyítsd be, hogy az
AD,
BC
egyenesek párhuzamosak!
Megoldás
111. Legfeljebb mekkora
n esetén helyezhet? el a sakktáblán
n vezér,
n
király és
n futó úgy, hogy ne üssék egymást?
Megoldás
112. Van-e 1995 db olyan nem
feltétlenül különböző szám, amelyek összege
megegyezik a szorzatukkal?
Megoldás
113. A és
B egy
1x9-es táblán egy bábúval játszik. A játék első részében
A
megszámozza a tábla mezőit az 1, 2, ... 9 számokkal. Ezután
B
választ egy mezőt, és arra helyezi fel a bábút. A játék második
részében is
A kezd. Felváltva lépnek a bábúval úgy, hogy
mindig az egyik szomszédos mezőre helyezik át. Vigyázni kell, mert
csak annyiszor lehet rátenni a bábút egy-egy mezőre, amekkora szám
van írva arra az adott mezőre. Az veszt, aki már nem tud lépni.
Kinek van nyer? stratégiája?
Megoldás
114. Bizonyítsd be,
hogy az
ABC háromszög síkjában egyetlen egy olyan
M
pont van, amelyre
MA +
BC =
MB +
AC =
MC
+
AB!
Megoldás
115. Aladár beírta az 1, 2, ... 81
számokat egy 9x9-es táblázat mezőibe. Boldizsár ki szeretné találni,
hogy melyik szám hol van. De csak úgy kérdezhet, hogy kijelöli a
táblázat egy rácsvonalak határolta négyzet alakú részét. Válaszul
Aladár felsorolja a kijelölt részben található számokat, a kedve
szerinti sorrendben.
Minimum hány kérdésre van szüksége Boldizsárnak
ahhoz, hogy biztosan kitalálja melyik szám hol van?
Megoldás
 Az
a oldalú négyzetet az AN, BK, CL, DM
egyenesekkel részekre bontottuk (lásd a 8. ábrát!). Bizonyítsd be,
hogy ha a sötét négyszög területe megegyezik a
halványabban satírozott háromszögek területének összegével,
akkor AM + BN + CK + DL = 2a!
Az
a oldalú négyzetet az AN, BK, CL, DM
egyenesekkel részekre bontottuk (lásd a 8. ábrát!). Bizonyítsd be,
hogy ha a sötét négyszög területe megegyezik a
halványabban satírozott háromszögek területének összegével,
akkor AM + BN + CK + DL = 2a!