28. A 17 emeletes ház földszintjén a liftnél 17 iskolás gyűlt össze, akik csupa különböző emeletre akarnak följutni. A lift azonban csak az egyik emeletig viheti föl őket, ahonnan már gyalog kell menniük. Tudjuk, hogy a diákoknak egyformán kellemetlen egy emeletnyit lefelé menni, de fölfelé emeletenként mindannyiuknak éppen két-szer olyan rossz. Melyik emelet gombját nyomják meg, hogy összességében majd a lehető legkevésbé legyen kellemetlen a gyaloglás?
Megoldás

29.

	1	2	3	4	5	6	7	8	N	D	V	L	K
1	*		0:0									3
2		*										4
3			*			1:1			0				1
4				*								4
5					*				1	1	2	2	2
6						*			0	1	3	1	4
7							*				3	0	3
8								*	0	0	4		5

2. ábra
N: nyert, D: döntetlen, V: vesztett mérkőzések száma;
L: lőtt gólok száma, K: kapott gólok száma.

Nyolc csapat egy olyan focibajnokságon vett részt, ahol mindegyikük négy mérkőzést játszott. A 2. ábrán egy hiányos táblázatot láthatsz, ami a bajnokságon lejátszott mérkőzések eredményeit mutatja. Fejezd be a táblázat kitöltését!
Megoldás

30.

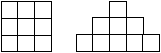
3. ábra

9 darab egyforma négyzet alakú kártyából először egy nagyobb négyzetet, azután egy piramist állítottunk össze (3. ábra). Úgy adódott, hogy bármely két olyan kártyalap, amelyeknek két közös sarka volt az első elrendezésben, egy közös sarokkal rendelkezett a második elrendezésben. Ráadásul ez a közös sarok már az első elrendezésben is közös volt. Bizonyítsd be, hogy ez lehetséges!
Megoldás

31. Helyezz el zárójeleket az alábbi összefüggés bal oldalán úgy, hogy teljesüljön az egyenlőség!
Megoldás

32. Az úti sakk-készletnek van egy kis pereme körben a tábla szélén, ami megakadályozza, hogy a figurák lecsússzanak. Az úti játékcsomaghoz dominó is tartozik, ami 28 méretre egyforma, éppen két mező letakarására képes darabból áll. El lehet-e helyezni a teljes dominókészletet a sakktáblán úgy, egyik darabot se lehessen elmozdítani a tábla síkjában?
Megoldás

33.

4. ábra

Egy szabályos háromszög P belső pontjából egyeneseket fektettünk, amelyek a három-szög csúcsain mennek át. Ezek az egyenesek a háromszöget 6 kisebb háromszögre osztják (4. ábra). Kiderült, hogy a satírozott háromszögek területének összege megegyezik a satírozatlan háromszögek területösszegével. Bizonyítsd be, hogy a P pont a háromszög egyik súlyvonalán helyezkedik el!
Megoldás

34. Az 1,5 érdekes szám, mert egyenlő a számjegyei összegének negyedével. Keress olyan számot, ami jegyei összegének nyolcadával egyezik meg!
Megoldás

35. Készíts egy 3x4-es téglalap alakú papíron bevágásokat úgy, hogy a papír ne essék szét, és össze lehessen hajtogatni belőle egy kétrétegű 1x1x1-es kockát!
Megoldás

36. Három diák fagylaltot vett. Csak papírpénze, azaz rubele volt mindegyiknek. Peti, akinek a legkevesebb pénze volt – mind-össze egy rubel [1] – két gombócot kért és elment. A másik két diák elhatározta, hogy minden pénzüket fagyira költik. Kiderült, hogy Karcsi 6 gombócot, míg Pisti 11 gombócot tudna venni, de ha összedobnák a pénzüket, akkor se futná 18 gombócra. Mennyibe került egy gombóc?
Megoldás

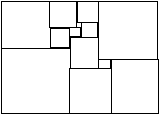
37. 50 gengszter egyszerre lő. Mindegyik a hozzá legközelebbi másik banditát célozza meg (illetve az egyik legközelebbit, ha többen is ugyanolyan messze vannak tő-le), és le is lövi. Legfeljebb hány gengszter maradhat így életben? (Úgy képzeljük, hogy a gengszterek a sík különböző pontjai.)
Megoldás

38. Mekkorák lehetnek annak a lehető legkisebb téglalapnak az oldalai, amelyet az 5. ábrán látható módon lehet egész oldal_ftnref1ú négyzetekre felbontani?
Megoldás

39. Milyen számokat jelölhetnek a betűk a kifejezésben, ha különböző betűknek különböző, azonos betűknek egyforma számok felelnek meg és tudjuk, hogy teljesül az egyenlőség?
Megoldás

40. Az ABC derékszögű háromszög AB befogóján az M, BC befogóján pedig az N pontot úgy vettük fel, hogy AM = CB és BM = CN. Bizonyítsd be, hogy az AN és CM szakaszok szöge 45^o!
Megoldás

41. Egy bohókás órásmester különleges órát készített. Szerkezete éjféltől egy óráig pontosan járt, de ezután az óramutató a percmutató segítségével forgott, míg a perc-mutató úgy járt, ahogy eredetileg az óramutatónak kellett volna. Ez így ment egy órán át, s azután a mutatók megint rendesen jártak. Persze csak egy óráig, mert a tréfás mester úgy tervezte gépét, hogy a mutatók óránként váltogatták sebességeiket!

Sorold föl az összes olyan időpontot, amikor e különleges óra a pontos időt mutatta!
Megoldás

42. 12 ember egy kerekasztalnál beszélgetett. Uzsonnaszünet után újra helyet foglaltak az asztalnál, de ekkor más sorrendben ültek le. Bizonyítsd be, hogy van a társaságban két olyan ember, akik között (az egyiktől a másikig az óramutató járása szerinti irányban) a második és az első esetben ugyanannyi ember ült.
Megoldás

43. Két párhuzamos egyenes közti sávra ráhelyeztek egy olyan négyzetet, amelynek az oldala éppen olyan hosszú, mint a sáv szélessége. A négyzet úgy helyezkedik el, hogy oldalai a sáv határoló egyeneseit összesen négy pontban metszik. Bizonyítsd be, hogy ebben az esetben a négy metszéspont közül a szemköztieket összekötve két olyan egyenest kapunk, amelyek szöge 45^o!
Megoldás

44. Harun-al-Rasid kalifa 10 erszényt adott ajándékba három udvari csillagjósának. A bölcsek kitapogatták, hogy az egyik erszény üres, a másikban 1 tallér van, a harmadikban 2 tallér, és így tovább egészen a tizedik erszényig, amelyikbe 9 tallért tett a kalifa. Husszein Husszlia elvett magának két erszényt. Abdurahman ibn Hottab és test-vére Omar Juszuf úgy osztották el egymás között a megmaradt erszényeket, hogy a többet szolgált és bölcsebb Abdurahmannak több pénz jusson. Omar Juszufra, hazafelé tartva, rablók támadtak és négy erszényt is elvettek tőle, így a kalifa ajándékból neki csak 10 tallérja maradt. Melyik erszényeket vette el magának Husszein Husszlia?
Megoldás

45. Korlátlan mennyiségű 1, 2, 5, 10, 20 és 50 kopejkásunk és 1 rubelesünk van. Bizonyítsd be, hogy ha az A kopejkányi összeget ki lehet fizetni B db pénzérmével, akkor a B rubelnyi összeg kifizethető A db pénzérmével!
Megoldás

46. Egy focibajnokságban 15 csapat vett részt. Mindegyik csapat mindegyikkel pontosan egyszer játszott. Lehetséges-e, hogy minden csapat ugyanannyiszor nyert, mint ahányszor döntetlent játszott? Mi a válasz 16 csapatos bajnokság esetén? És 17 csapatosnál?
Megoldás

47.

Arkagyij Gajdar meséjében, a ?Forró kő”-ben Ivaska Kudrjaskin talál egy követ, amire rejtélyes jeleket véstek: két keresztet, három farkincát, egy karikás pálcikát és négy vesszőcskét (6. ábra). Tegyük fel, hogy ez egy titkosírással lejegyzett tízjegyű négyzetszám. Melyik számjegyet jelöli a karikás pálcika?
Megoldás

48. Az ABC, PQR szabályos háromszögek úgy helyezkednek el a síkban, hogy a C csúcs a PQ szakaszra, míg az R csúcs az AB szakaszra illeszkedik. Bizonyítsd be, hogy — a jelöléstől függően — AP és BQ vagy pedig AQ és BP párhuzamosak!
Megoldás

49. A 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 számjegyek mindegyikét pontosan egyszer felhasználva készíts két olyan ötjegyű számot, melyek szorzata a lehető legnagyobb!
Megoldás

50. Ha a sakktáblát 2x1-es dominókkal fedjük le, akkor bármelyik főátló nyolc mezőjét összesen nyolc dominó takarja le. Ezeknek a dominóknak a másik fele vagy a fő-átló alatt, vagy a fölött helyezkedik el. Bizonyítsd be, hogy akárhogyan is fedjük le a sakktáblát, az átlótól "felfelé kilógó” és a "lefelé kilógó” dominók száma mindig 4-4!
Megoldás

51. Az asztalon áll egy kocka, amit elgörgethetünk úgy, hogy egy lépésben az éppen az asztallapra fekvő oldalának egyik éle körül 90^o-kal elforgatjuk. El lehet-e érni, hogy minden él körül pontosan egyszer forgatva a kocka úgy gördüljön, hogy legvégül éppen eredeti helyére kerüljön vissza?
Megoldás