
Megoldások
Az 1991/92. tanév
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
N |
D |
V |
L |
K |
|
1 |
* |
0:0 |
1:0 |
1:0 |
1:0 |
3 |
1 |
0 |
3 |
0 | |||
|
2 |
* |
1:0 |
1:0 |
1:0 |
1:0 |
4 |
0 |
0 |
4 |
0 | |||
|
3 |
0:0 |
* |
0:0 |
1:1 |
0:0 |
0 |
4 |
0 |
1 |
1 | |||
|
4 |
* |
1:0 |
1:0 |
1:0 |
1:0 |
4 |
0 |
0 |
4 |
0 | |||
|
5 |
0:1 |
0:0 |
0:1 |
* |
2:0 |
1 |
1 |
2 |
2 |
2 | |||
|
6 |
0:1 |
0:1 |
1:1 |
0:1 |
* |
0 |
1 |
3 |
1 |
4 | |||
|
7 |
0:1 |
0:1 |
0:0 |
0:1 |
* |
0 |
1 |
3 |
0 |
3 | |||
|
8 |
0:1 |
0:1 |
0:1 |
0:2 |
* |
0 |
0 |
4 |
0 |
5 |
19. ábra
N: nyert, D: döntetlen,V: vesztett mérkőzések száma;
L: lőtt gólok száma,
K: kapott gólok száma.


A = x + 2y + 5z + 10t + 20u + 50v + 100w,
B = x + y + z + t + u + v + w,
ahol x, y, z, t, u, v rendre az 1, 2, 5, 10, 20 és 50 kopejkások számát, míg w a rubelesek mennyiségét jelöli. A második egyenlet százszorosát így is írhatjuk:100B = 100x + 50(2y) + 20(5z) + 10(10t) + 5(20u) + 2(50v) + 1(100w).
Jelölje most x a rubelesek 2y, 5z, 10t, 20u, 50v és 100w pedig rendre az 50, 20, 10, 5, 2, 1 kopejkások számát. Mit fejez most ki az első és a harmadik egyenlet?1 122 250 000 = 33 5002,
4 422 250 000 = 66 5002.
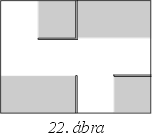
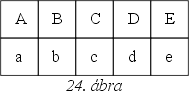 Lehetséges. Egy megoldás: mozgassuk a kockát
egy 10 négyzetből álló téglalapban (lásd a 24. ábrát), ahol a kis
négyzetek oldalai olyan hosszúak, mint a kocka élei. A görgetés
útvonala:
Lehetséges. Egy megoldás: mozgassuk a kockát
egy 10 négyzetből álló téglalapban (lásd a 24. ábrát), ahol a kis
négyzetek oldalai olyan hosszúak, mint a kocka élei. A görgetés
útvonala:
![]()