Megoldások
Az 1992/93.
tanév
52. Nem lehetséges. Határozzuk meg
először, hogy hány levél (tallér) nő ki egy-egy fán reggelente. Legyen az
a szám n. Mivel keddig 4 éjszaka van, péntekig pedig 7, így a
feltételek szerint 5n4 < 1992
≤
5n7, azaz n = 3, vagy 4.
n = 3 esetén az érmék számának
paritása nem változik egyik napról a másikra, hiszen mindig 1 tallérból
lesz 3.
n = 4 esetén pedig az érmék számának
3-as maradéka marad változatlan. Mivel 1992 2-es és 3-as maradéka is
különbözik 5 megfelelő maradékától, így nem lehetséges, hogy a Bendegúznak
épp 1992 tallérja legyen, de reméljük ettől nem lesz nagyon szomorú.
53. Vegyük észre, hogy a, b,
c mindegyike osztja a másik kettő szorzatát. Ebből következik,
hogy, ha az abc szorzat osztható p-vel, akkor
pn-nel is osztható, valamely n > 1 számmal. De
ekkor biztosan találhatók olyan x, y nemnegatív egészek,
amelyek-re pn =
p3x.p2y, ami
igazolja a feladat állítását.
54.
n.(n + 1).(n +
2).(n + 3)/24.
55. Ne mérgelődjön,
a fordító is megszenvedte ezt a feladatot. Bizonyára nem gondolt, az
egyszerű tényre, miszerint a víziló növényevő, nem eszik halat. Ezt
felhasználva egyszerűen adódik a megoldás: a bálna 16, a pelikán 12, a
rozmár 9 halat evett meg.
56.
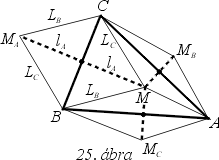
Legyen az
M pont középpontos tükörképe az
AC, CB, BA oldalak
felezőpontjaira vonatkozóan rendre
MB, MA,
MC (lásd a 25. ábrát).
AMC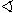
,
CMB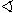
és
BMA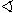
közül
legalább az egyik, ábránkon épp
CMB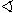
, legfeljebb
120
o. Tekintetbe véve az
BMC és az C
MMA
háromszögeket, felír-hatjuk, hogy 60
o ³ MCB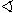
+
MBC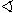
=
MCMA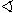
. Ez azt
jelenti, hogy az
CMMA háromszögben van
MMA-nél nem rövidebb oldal, tehát 2
lA
£ max[
LB,
LC].
57.
3 vagy 4
csapat.
58. 2029 részes.
A sorozatot összesen öt
évben vetítették. Az egyik évben vetített részek száma az előző évben
bemutatott részek számának 3/5, vagy 7/5 –szöröse. Ezért az első, az
1988-adik évben vetített részek száma 54 = 625 többszöröse kell
legyen. Legfeljebb 2.366 = 732 részt vetíthettek egy évben,
tehát pont 625 részt láthattak a nézők 1988-ban. A második évben
ugyanezért csak 625.3/5 = 375 epizód lehetett. Az adatokból
kiderül, hogy a harmadik év folyamán mutatták be az 1230-adik részt. Ezért
zárható ki, hogy 1990-ben csak 375.3/5 részt mutattak volna be,
hiszen ebben az esetben az első három év részeinek száma csak 1225 lenne.
Ebből tudhatjuk, hogy 1990-ben 375.7/5 = 525 rész volt látható,
köztük az 1230-adik valamikor az év első felében. 1991-ben csak
525.3/5 = 315 részt vetítettek, 1992-ben pedig
315.3/5 = 189-et, hiszen 315.7/5 = 441 rész esetén
az utolsó előadás az év második felébe esett volna.
59. 970 299.
60. A piros
szakaszok mentén vágjunk bele ollóval a kocka felületébe! Ha a feladat
állítása nem igaz, akkor a felület nem esik szét. Ezért, ha a felületet
teljesen föl akarjuk darabolni 24 kis négyzetére, akkor még legalább 23
szakaszt végig kell vágnunk. A megmaradt szakaszok száma azonban már csak
22, hiszen eredetileg összesen 4.24/2 = 48 szakasz volt.
61. Az általánosítás
így fogalmazható: az An = (n +
1).(n + 2)......(2n –
1).2n szám osztható 2n-nel, de
2n+1-nel már nem osztható. A bizonyítás
teljes indukcióval történhet, az
Ak+1/Ak = 2.(2k + 1)
összefüggés felhasználásával.
62. Be lehet írni a
számokat a feltételnek megfelelő módon. Egy lehetséges megoldást kapunk,
ha a következőképpen járunk el: először is sakktáblaszerűen színezzük a
lapot. Ezután beírjuk balról jobbra sorban a fehér mezőkbe a az 1, 2, ...
677 számokat, amíg lehet az első sorba, utána a másodikba stb. Ezután a
678-tól 1353-ig terjedő számokat írjuk be a sötét mezőkbe, de most az alsó
sor leghátsó oszlopából indulunk el és jobbról, balra illetve fölfelé
haladunk.
63. Nem lehet.
Legyen a mikrobuszok és a Volgák eredeti száma
m illetve
v.
Az első átrendezés úgy is fölfogható, hogy minden járműből egy-egy gyerek
kiszállt, így
m +
v Î{33; 28; 23; 18}
hiszen a három új járműbe
33, 28, 23, vagy 18 diák ült be attól függően, hogy 3, 2, 1 vagy 0
mikrobusz volt az újonnan érkezettek között. További járművek érkezése
esetén minden eredeti járműből és a 3 később érkezettből is egy-egy gyerek
szállna ki, így
m +
v + 3 = 5v2 + 10m2,
ahol
v2
jelöli szükséges Volgák,
m2 pedig a mikrobuszok
számát. Itt a jobboldal az 5 többszöröse, míg a baloldalról ez egyik
esetben sem mondható el.
64. Mindkét esetben
az tud nyerni, aki elsőnek vesz el gyufát.
65. A 7 áll
az 1993. helyen.
66. Egyik sem lehet.
A mutató végpontjának sebessége arányos a mutató hosszával és
szögsebességével is. Ha r, illetve R jelöli
az óra-, illetve a percmutató hosszát és az óramutató végpontjának
sebessége kr, akkor a percmutató végének sebessége
12.kR. A két mutató egymáshoz képesti relatív
sebességének minimuma 12kR – kr, ami akkor áll elő, amikor a
mutatók egyállásúak. Relatív sebességük maximuma 12kR + kr,
amikor ellentétes állásúak. Ebből látható, hogy a minimális és a maximális
relatív sebességek aránya 11/13 és 1 között van, hiszen R >
r. Az adott esetekben azonban
8/10 < 11/13 és 10/12
< 11/13.
67. Legyen BC
AB! Forgassuk el B körül 90o-kal a C
rácspontot! A CC' szakasz O felezőpontja az AB
szakasz belsejében van. Tükrözzük B-t O-ra! Bizonyítsuk be,
hogy így rácspontot kapunk, ami nem lehet más, mint A!
68. Bizonyítandó,
hogy a4k+1 – a osztható 10-zel, bármely
természetes számokat is jelöl a és k!
69. Igen, ki lehet
találni.
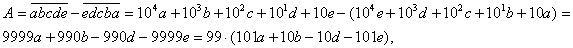
tehát A utolsó három
jegyét úgy kell elölről kiegészíteni, hogy osztható legyen 99-cel.
Azt
kell megmutatnunk, hogy ez csak egyféleképpen lehetséges.
Valóban, az első két
számjeggyel való kiegészítés a 0, 1000, 2000, ... 99000 számok egyikének
hozzáadását jelentik. Ezek csupa különböző maradékot adnak 99-cel
osztva, kivéve a 0-t és a 99000-t. Tehát az első két számjegy
egyértelműen adódik, ha az adott háromjegyű szám nem osztható 99-cel.
Befejezésül csak annak kell
utánajárni, hogy ötjegyű szám és megfordítottjának
különbségeként nem kaphatunk olyan ötjegyű
számot, mely 99-cel kezdődik
70. Hét olyan
számhármas van, ami kielégíti az egyenletet:
(2; 2; 2), (4; 2¸1), (4;
1¸2), (2; 4¸1), (2; 1¸4), (1; 4¸2) és (1; 2¸4).
71. Tekintsük úgy,
mintha a könyvek körben lennének, azaz, mintha a jobb szélső könyv után
jobbra a bal szélső következne. Ha először kivesszük és előre tesszük a
harmadik könyvet, majd kétszer a nyolcadik helyen levő könyvet
tesszük előre, akkor, végül is, a harmadik könyv az eredeti helyére kerül
vissza, az összes többi pedig ciklikusan arrébb helyeződik. E
háromlépéses művelet megfelelő számú alkalmazásával elérhető, hogy a
helyben maradó könyv egy tetszőleges előre választott könyv mögé
kerüljön. Ennek alapján már könnyen bizonyítható az állítás.
72. A 35 964.
74. Legfeljebb 9.
Egy nem szökőévben lehetséges 9 születésnap pld. feb. 1., márc. 1., május
1., 3., 10., 17., 24. és 31, valamint nov. 1. Szökőévben megfelelő
dátumok: jan. 1., ápr. 1., júl. 1., továbbá szeptember 1., 2., 9., 16.,
23. és 30. Bővebben lásd a Bergengóc példatárban a 87. feladat megoldását
a 160-162. oldalakon.
75.
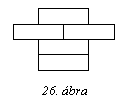
Össze lehet állítani. Pld. úgy, ahogyan a 26. ábrán látható.


![]()
![]() +
BMN
+
BMN![]() = BAC
= BAC![]() +
BCA
+
BCA![]() > NAC
> NAC![]() +
MCA
+
MCA![]() = MNA
= MNA![]() +
NMC
+
NMC![]() .
.