Az 1993/94. tanév
76. Bizonyítsd be, hogy 1993
.1995
3
- 1994
.1992
3 egy egész szám köbe!
Megoldás
77. El lehet-e helyezni 8
pontszerű súlyt, melyek tömege rendre 1, 2, ... 8 kg, egy kocka
nyolc csúcsába úgy, hogy tömegközéppontjuk a kocka
középpontjával egyezzék meg?
Megoldás
78. Szerkessz háromszöget
körző és vonalzó segítségével, ha adott a súlypontja, köréírható
körének középpontja, továbbá a köréírt körnek és
az egyik szögfelezőnek, a csúcstól különböző
metszéspontja!
Megoldás
79. Két egymást követő szám
mindegyike megegyezik saját számjegyei köbének összegével.
Melyek ezek a számok?
Megoldás
80. Melyik az a legkisebb
x
pozitív szám, amelyre
a)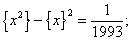
b)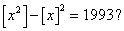
Itt [a] az a szám egészrészét, tehát a
legnagyobb a-nál nem nagyobb egész számot jelöli, míg {a}
= a – [a], az a törtrésze.
Megoldás
81. Néhány évvel a
Délnyugati Birodalom széthullása után a területén létrejött
16 hercegség mindegyike 3 másikkal barátságban élt, a többivel
pedig ellenségeskedett. A hajdani birodalom szomszédságában található
8 állam elhatározta, hogy segítséget nyújt a viszályokban tönkrement
hercegségeknek, méghozzá mindegyik állam 2 egymással barátkozó
hercegségnek nyújt támogatást. Meg lehet-e szervezni minden esetben a
segélyezést úgy, hogy mindegyik hercegség részesüljön
belőle?
Megoldás
82. Mely
m és
n
természetes számokra teljesül a
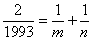
összefüggés?
Megoldás
83. Az 1x50-es tábla
50. mezőjén áll egy bábú. Ketten játszanak, felváltva lépnek a
bábúval. Egy lépésben 1 vagy 2 mezővel lehet arrébb helyezni a bábút
bármelyik irányban. Tilos olyan mezőre lépni, amelyiken egyszer már
volt a bábú. Az veszt, aki nem tud lépni.
Kinek van nyerő stratégiája, a kezdőnek, vagy
ellenfelének?
Megoldás
84. Van-e olyan 11-re
végződő szám, ami osztható 11-gyel és számjegyeinek összege 11?
Megoldás
85. Az
ABC háromszög
A,
B,
C csúcsaiból rendre meghúztuk a háromszög
egy-egy szögfelezőjét, súlyvonalát és magasságát. E három
egyenes egy
O pontban metszette egymást. Bizonyítsd be, hogy
amennyiben
AB a háromszög leghosszabb oldala, akkor
BO
>
AO, ha viszont
AB a legrövidebb oldal, akkor
BO <
AO!
Megoldás
86. Egy 4x4-es négyzet egységnyi
oldalú négyzetekre van osztva. A kis négyzetek oldalai egy rácsot
alkotnak. Ki lehet-e rakni ezt a rácsot 8 db 5 egység hosszúságú
cérnából? És 5 db 8 egység hosszúból?
Megoldás
87. Malacka és Zsebibaba ugyanazt
az egész számot osztják el maradékosan. Zsebibaba 8-cal, Malacka
9-cel oszt. A Zsebibaba által kapott hányados és a Malackánál kapott
maradék összege 13. Milyen maradékot kapott Zsebibaba?
Megoldás
88. Lehet-e valamely egész helyen
éppen 1994 egy olyan egész együtthatós
P(
x)
polinomnak az értéke, amelyre
P(0) = 1995 és
P(1) =
P(5) = 0?
Megoldás
89. Infláciban gyakran emelik a
villamos közlekedés díját. A jegy árát ilyenkor a jegy nélkül
utazókra kirótt büntetés mértékére emelik, a büntetés pedig
mindig az éppen érvényes jegy árának 10-szerese. Makacs Tamás elvi
kérdést csinál abból, hogy ne vegyen jegyet, így már 9-szer büntették
meg. Ráadásul az egyik alkalommal fizetés közben elejtett, és
így elvesztett egy “nagy értékű” bankót. Így Tamásnak
eddig 23450 Ft-ja ment rá a villamosozásra.
Hány forintos bankót vesztett el Tamás?
Megoldás
90. Egy 6x6-os táblázat
mezőibe úgy írtunk be 36 –nem feltétlenül különböző-
számot, hogy a 22 átló mindegyikében ugyanakkora a számok összege.
Mekkora lehet ez az összeg? (Az átlókban 1, 2, 3, 4, 5 vagy 6
mező áll.)
Megoldás
91. Melyik a nagyobb,
(1
.3
.5
.7
....
.1993)
2
vagy 1993
997?
Megoldás
92.
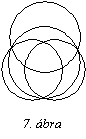
4 kör úgy helyezkedik el, ahogyan az a 7. ábrán látható. A
körökön belül létrejött 10 tartományba úgy
kell beírni a 0, 1, ... 9 számokat, hogy az egyes körökön
belüli számok összege egyenlő legyen egymással. Legfeljebb
mekkora lehet ez az összeg?
Megoldás
93. Az
ABC egyenlőszárú
háromszög
BC szárán adott az
M, az
MC
szakaszon pedig az
N pont úgy, hogy
MN =
AN.
Tudjuk, hogy a
BAM és az
NAC szögek egyenlőek.
Határozd meg az
MAC szög nagyságát!
Megoldás
94. Bizonyítsd be, hogy végtelen
sok olyan nem nullára végződő pozitív egész szám van, amelyben a
jegyek összege megegyezik a szám négyzete jegyeinek összegével!
Megoldás
95. Helyezz el 16 fehér és 16
fekete bábút a sakktábla különböző mezőire úgy, hogy
minden sorban, minden oszlopban és mind a harminc átlóban a fekete
bábúk száma megegyezzék a fehérekével! (Az egyes átlókban 1, 2, 3,
... 7, vagy 8 mező áll.)
Meg lehet-e ugyanezt tenni 15 fekete és 15 fehér
bábúval?
Megoldás
![]()
![]()
![]()
![]()
