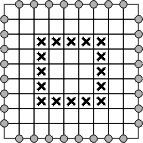
Megoldások
Az 1994/95. tanév
n = 2a . (2m + 1) = (2a - m) + ... + (2a - 1) + 2a + (2a + 1) + ... (2a + m).
Ha viszont 1 £ 2a £ m, akkor az alábbi 2.2a tagú összeg lesz jó:n = (m - 2a + 1) + ... + m + (m + 1) + ... + (m + 2a).
A még kimaradt m = 0 esetben, azaz n = 2a esetén nem lehetséges
(l + 1) + (l + 2) + ... + (l + k) = 2a
alakú előállítás (k > 1), mert a baloldal összegzése, és 2-vel szorzás után
(2l + k + 1).k = 2a+1
adódna, ahol a baloldalon két különböző paritású szám szorzata áll. (Lásd még: Bergengóc példatár 59. feladat, 110-114. oldal.)
|
2. mérés |
3. mérés |
4. mérés |
a |
b |
c |
d |
e |
f |
|
2. mér. |
3. mér. |
4. m. |
a |
b |
c |
d |
e |
f |
|
|
|
e>d |
1 |
0 |
1 |
0 |
1 |
0 |
|
|
|
e>f |
1 |
1 |
1 |
0 |
1 |
0 |
|
|
ead>bcf |
e=d |
11 |
1 |
1 |
1 |
1 |
0 |
|
|
cb>ef |
e=f |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
e |
1 |
0 |
0 |
1 |
0 |
0 |
|
|
|
e |
1 |
1 |
1 |
0 |
0 |
1 |
|
|
|
e>d |
nem lehetséges |
|
|
|
a>c |
1 |
0 |
0 |
0 |
0 |
0 | |||||
|
ac>ef |
ead=bcf |
e=d |
1 |
0 |
1 |
0 |
0 |
0 |
|
ac>bd |
cb=ef |
a=c |
1 |
1 |
1 |
0 |
1 |
1 |
|
|
|
e |
1 |
1 |
1 |
1 |
0 |
0 |
|
|
|
a |
nem lehetséges | |||||
|
|
|
b>f |
0 |
1 |
1 |
0 |
0 |
0 |
|
|
|
e>f |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
ead |
b=f |
1 |
1 |
1 |
1 |
0 |
1 |
|
|
cb |
e=f |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
|
b |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
|
e |
1 |
0 |
0 |
0 |
0 |
1 |
|
|
|
a>b |
1 |
0 |
0 |
1 |
1 |
0 |
|
|
|
a>f |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
e>f |
a=b |
nem lehetséges |
|
|
a>e |
a=f |
1 |
1 |
0 |
0 |
0 |
1 | |||||
|
|
|
a |
0 |
1 |
1 |
0 |
1 |
0 |
|
|
|
a |
nem lehetséges | |||||
|
|
|
a>b |
1 |
0 |
1 |
0 |
1 |
1 |
|
|
|
a>f |
1 |
1 |
0 |
0 |
1 |
0 |
|
ac=ef |
e=f |
a=b |
mind jó v. rossz |
|
ac=bd |
a=e |
a=f |
1 |
1 |
0 |
0 |
1 |
1 | |||||
|
|
|
a |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
|
a |
nem lehetséges | |||||
|
|
|
a>b |
1 |
0 |
0 |
1 |
0 |
1 |
|
|
|
|
||||||
|
|
e |
a=b |
nem lehetséges |
|
|
a |
|
nem lehetséges | ||||||||||
|
|
|
a |
0 |
1 |
1 |
0 |
0 |
1 |
|
|
|
|
||||||
|
|
|
b>f |
0 |
1 |
0 |
1 |
1 |
0 |
|
|
|
e>f |
1 |
1 |
0 |
1 |
1 |
0 |
|
|
ead>bcf |
b=f |
0 |
0 |
0 |
0 |
1 |
0 |
|
|
ad>ef |
e=f |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
b |
1 |
0 |
0 |
1 |
1 |
1 |
|
|
|
e |
1 |
1 |
0 |
1 |
0 |
1 |
|
|
|
b>f |
nem lehetséges |
|
|
|
a>b |
nem lehetséges | ||||||||||
|
ac |
ead=bcf |
b=f |
0 |
1 |
0 |
1 |
1 |
1 |
|
ac |
ad=ef |
a=b |
1 |
1 |
0 |
1 |
1 |
1 |
|
|
|
b |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
|
a |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
e>d |
0 |
1 |
1 |
0 |
1 |
1 |
|
|
|
e>f |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
ead |
e=d |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
ad |
e=f |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
|
e |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
|
e |
0 |
1 |
0 |
0 |
0 |
1 |
(a – 3).(a – 1).(a + 1).(a + 3) + 16 = (a2 – 5)2
azonosságból.