Az 1996/97. tanév
136. Hány néggyel
osztható tagja van az alábbi sorozatnak?
12 + 34, 56 + 78, 910 + 1112,
1314 + 1516, ...
Megoldás
137. Az
ABC derékszögű háromszögben meghúztuk a hegyesszögek
AP,
BQ szögfelezőit, majd az
ACP,
BCQ háromszögek
C-ből induló
CM,
CN súlyvonalait. Bizonyítsd be, hogy
a
CMP,
CNQ szögek összege megegyezik az
MPQ,
NCM és
PQN szögek összegével!
Megoldás
138. Kirabolták a
tudománynépszerűsítő folyóirat, a Kvant szerkesztőségét. A tettesek
elvittek egy nagy köteget a lap legfrissebb számából, amivel több, mint
két és fél millió dollár kárt okoztak a kiadónak. Később ugyan sikerült
elfogni a banditákat, de addigra már a szám egyheted részét eladták. A
megmaradt példányokat a rendőrség visszajuttatta a kiadónak. A kárt
helyrehozandó, 60 centtel drágábban adták a megszokottnál a lapot, de ez
még mindég nem fedezte a veszteséget. Szerencsére, egy lelkes
feladatmegoldóból bankárrá lett olvasó támogatásképp 1 dollárral drágábban
vette meg a folyóiratot, így a hiány bőven kárpótolva lett.
Mennyibe került a lap eredetileg, a
kényszerű áremelés előtt?
Megoldás
139. Bizonyítsd be, hogy,
ha
(x + y +
z)( xy + yz + zx) = xyz,
akkor
(x +
y).(y + z).(z +
x) = 0!
Megoldás
140. Egy berendezés 49
gombból áll, mindegyiknek két lehetséges állapota van: vagy világít, vagy
nem. A gombok 7 sorban és 7 oszlopban helyezkednek el. Egy gomb
megnyomásakor ez a gomb, és vízszintes, függőleges ás átlós szomszédai
egyszerre váltanak: az addig világítóak kialszanak, a kikapcsoltak
meggyulladnak. Bizonyítsd be, hogy el lehet oltani az összes gombot,
akárhány és akármelyik világított is eredetileg közülük!
Megoldás
141. Van egy készlet
dominónk. E dominókra a 0, 1, 2, ...
n számok vannak írva,
mindegyik dominóra két szám. Készletünk teljes, azaz a fent említett
számokból képzett bármely számpárhoz pontosan egy
olyan dominó található, amelyre az a két szám van fölírva. A készletből
maximálisan hány dominó rakható ki az asztalra a játék szabályainak
megfelelően?
Megoldás
142. Keresd meg az összes
olyan természetes számot, amit nem lehet fölírni néhány (legalább két)
egymást követő egész szám összegeként!
Megoldás
143. Bizonyítsd be, hogy
ha egy tizenkilenszög minden belső szöge a 10
o többszöröse,
akkor a tizenkilencszögnek van két párhuzamos oldala!
Megoldás
144. Öt bájos leány,
Anna, Bella, Cili, Dóri és Enikő jutott be a "Miss Kvant 96” verseny
döntőjébe. Az egyik újságíró megkérdezte Enikőt:
Ki az idősebb, te,
vagy Bella? Enikő így válaszolt:
Ha öregebb vagyok Annánál, akkor
Bellánál is öregebb vagyok, viszont fiatalabb vagyok, mint Cili. Ha
azonban nem vagyok idősebb Bellánál, akkor fiatalabb vagyok, mint Dóri. Ha
korban Dóri megelőz és Annánál öregebb vagyok, akkor nem vagyok Cilinél
fiatalabb. Ha Dóri idősebb nálam és nem vagyok fiatalabb Bellánál, akkor
öregebb vagyok, mint Anna.
Mi a helyes válasz a felettébb
udvariatlan újságírói kérdésre?
Megoldás
145. Nyolc különböző
méretű könyv áll egymás mellett egy polcon. E nyolc könyvvel a
következő eljárást végezzük el:
vesszük a balról számítva két első
könyvet, összehasonlítjuk a nagyságukat, és a nagyobbat a balról harmadik,
a kisebbet az utolsó helyre tesszük be.
Ezután újból kiemeljük a balról számítva
két első könyvet és azokkal hajtjuk végre az előzőleg már leírt eljárást.
Így haladunk tovább, a leírt eljárást ismételgetve.
a) Ki lehet-e mindig találni, a
fenti folyamat, lépésenkénti eredményének ismeretében, hogy melyik a
legnagyobb könyv?
b) Van-e a könyveknek olyan kezdeti
elrendezése, hogy az abból induló folyamat eredményeinek ismeretében
megállapítható a könyvek nagyságrendi sorrendje?
Megoldás
146. Bizonyítsd be, hogy
n 2 esetén, azok között a számok között, amelyek
n db
egyesből és 1 db hetesből állnak van legalább egy összetett szám!
Megoldás
147.
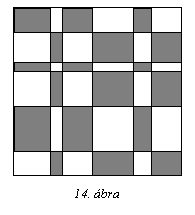 Egy négyzetet az oldalaival
párhuzamos vágásokkal téglalapokra osztottunk. Ezeket a
téglalapokat sakktáblaszerűen feketére és fe-hérre színeztük (14.
ábra). Kiderült, hogy a fekete téglalapok összterülete megegyezik a
fehér téglalapokéval. Bizonyítsd be, hogy a fekete
téglalapok át-rendezhetők úgy, hogy együtt egy téglalapot
alkossanak!
Egy négyzetet az oldalaival
párhuzamos vágásokkal téglalapokra osztottunk. Ezeket a
téglalapokat sakktáblaszerűen feketére és fe-hérre színeztük (14.
ábra). Kiderült, hogy a fekete téglalapok összterülete megegyezik a
fehér téglalapokéval. Bizonyítsd be, hogy a fekete
téglalapok át-rendezhetők úgy, hogy együtt egy téglalapot
alkossanak!
Megoldás
148. Induljunk ki egy
A0 természetes számból, és szorozzuk össze számjegyeinek
összegével! Jelöljük az így kapott számot
A1-gyel!
A1 és számjegyei összegének szorzata legyen
A2, és így tovább. Keresd meg az összes olyan
természetes számot, amelyből kiindulva valamelyik
Ak
szám, és így az összes utána következő is, 1 lesz!
Megoldás
149. Adottak a síkon az
ABC,
ACO szabályos háromszögek. Tekintsük azt az
O
középpontú kört, amely áthalad az
A,
C pontokon! Bizonyítsd
be, hogy e kör bármely
M pontjára
MA2 +
MC2 =
MB2!
Megoldás
150. Egy négyzetet
felosztottunk 19x19 kisebb négyzetre, és a kis négyzetek közül 95-öt
besatíroztunk. Bizonyítsd be, hogy van olyan 3x5-ös téglalap alakú rész,
amelyben legfeljebb 3 kis négyzet van besatírozva! Mutasd meg, hogy
96 ügyesen választott négyzet satírozásával elérhető, hogy minden 3x5-ös
téglalapban legalább 4 satírozott négyzet legyen!
Megoldás
151.
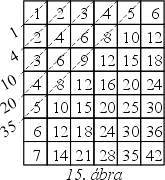
Pithagorasz táblázata (a
szorzótábla) úgy van kitöltve, hogy a bal fölső sarkától számított
n-edik sor és
m-edik oszlop találkozásában található mezőben
az
nm szorzat értéke áll. Tekintsük az azonos átlóban álló számok
összegeit! (A 15. ábrán láthatók az 1., 2., 3., 4., 5., átlóban kapott
összegek) Bizonyítsd be, hogy az 1996. átlóban álló számok összege 1996-ra
végződik!
Megoldás
152. Egy
a oldalú
négyzet egyik csúcsából indulva állandó sebességgel halad a négyzet
kerületén az
A pont. Ugyanakkor, és ugyanabból a csúcsból
ugyanabban az irányban elindulva, de négyszer akkora állandó sebességgel
mozog a
B pont. Legyen
M a mozgó
AB szakasz mozgó
felezőpontja. Mekkora utat jár be az
M pont addig, amíg
A
visszaér abba a csúcsba, amelyikből indult?
Megoldás
153. Egy egész számból a
következő módon képezhetünk egy újabb számot: kiválasztjuk tízes
számrendszerbeli alakjának egyik jegyét és azt kivonjuk a számból vagy
pedig hozzáadjuk. Eljuthatunk-e ennek a képzési szabálynak az ismételt
alkalmazásával 1970-től 97-ig?
Megoldás
154. A sakktábla melyik
4x4-es négyzetét vágjuk ki, ha azt akarjuk, hogy a megmaradó részt
lefedhessük 1x3-as dominókkal?
Megoldás
155. Adott egy szabályos
háromszög, amelyben elhelyezhető 5 egymást nem metsző egységsugarú kör.
Bizonyítsd be, hogy ebben a szabályos háromszögben 6 egymást nem metsző
egységsugarú kör is
elfér!
Megoldás
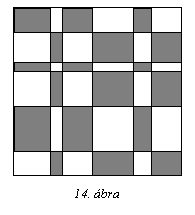 Egy négyzetet az oldalaival
párhuzamos vágásokkal téglalapokra osztottunk. Ezeket a
téglalapokat sakktáblaszerűen feketére és fe-hérre színeztük (14.
ábra). Kiderült, hogy a fekete téglalapok összterülete megegyezik a
fehér téglalapokéval. Bizonyítsd be, hogy a fekete
téglalapok át-rendezhetők úgy, hogy együtt egy téglalapot
alkossanak!
Egy négyzetet az oldalaival
párhuzamos vágásokkal téglalapokra osztottunk. Ezeket a
téglalapokat sakktáblaszerűen feketére és fe-hérre színeztük (14.
ábra). Kiderült, hogy a fekete téglalapok összterülete megegyezik a
fehér téglalapokéval. Bizonyítsd be, hogy a fekete
téglalapok át-rendezhetők úgy, hogy együtt egy téglalapot
alkossanak!