Jele:
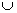
Példa:
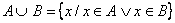
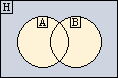
Jele:
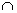
Példa:
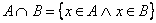
Jele:
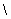
Példa:
Jele:
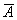
Példa:
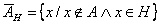
A 'C'-sek Lexikona
Halmazok
|
Két halmaz egyesítése (uniója) Jele: 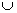 Példa: 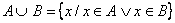
|
|
|
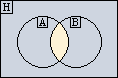
Két halmaz közös része (metszete) Jele: 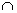 Példa: 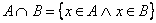
|
|
|
Két halmaz különbsége Jele: 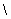 Példa: 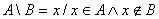
|
|
|
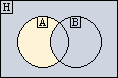
Egy halmaz kiegészítő-halmaza (komplementere) Jele: 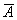 Példa: 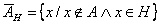
|
|
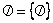 Az első áthúzott karika magát az üres halmazt jelöli, míg a második az üres halmaznak az eleme, tehát az üres halmaznak egy eleme van. |
|
|
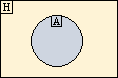
A részhalmaza B-nek, ha A minden eleme eleme B-nek is. Jele: 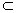 Példa: ha 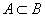 , akkor , akkor 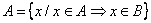 A valódi részhalmaza B-nek, ha B-nek van olyan eleme, ami nem eleme A-nak. |
|
|
A szimmetrikus különbséget háromféle egyenlettel is ki tudjuk fejezni: 1. 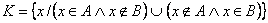 2. 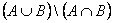 3. 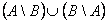
|
|
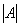
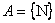 , akkor
, akkor 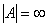 .
.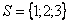 , akkor
, akkor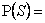
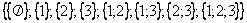 ,
,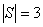 és
és 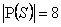 .
.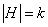 , akkor
, akkor 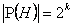 .
.
Számelmélet
A pozitív egész számok három csoportja
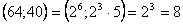
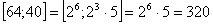
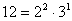 , tehát
, tehát
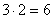 osztója van 12-nek.
osztója van 12-nek.
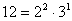 esetén:
esetén: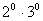 ;
;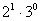 ;
;
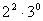 ;
;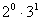 ;
;
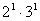 ;
;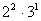
Az Euklidesi szerkesztés lépései
Az Euklidesi szerkesztés megengedett lépései

| 1 | + | 2 | + | 3 | + | ... | + | (n-1) | + | n |
| n | + | (n-1) | + | (n-2) | + | ... | + | 2 | + | 1 |
| n+1 | n+1 | n+1 | n+1 | n+1 |
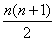 .
.
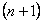 .
Mivel n elem van, a két sor összege
.
Mivel n elem van, a két sor összege 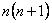 , de minden számot kétszer számoltunk,
tehát 1-től n-ig a számok összege
, de minden számot kétszer számoltunk,
tehát 1-től n-ig a számok összege 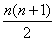 .
.
A háromszög nevezetes vonalai
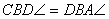
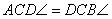
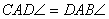
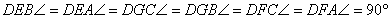
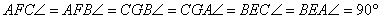
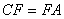
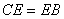
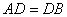
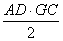 . Ez a területe a DBC háromszögnek is, mert alapjuk
(AD = DB) és hozzátartozó magasságuk (GC) egyenlő. Ugyanez vonatkozik az AEC
és AEB, CFB és FBA háromszögekre.
. Ez a területe a DBC háromszögnek is, mert alapjuk
(AD = DB) és hozzátartozó magasságuk (GC) egyenlő. Ugyanez vonatkozik az AEC
és AEB, CFB és FBA háromszögekre.
A külső szögfelező
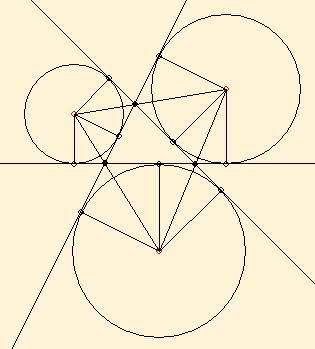
Egybevágósági transzformációk
| Tulajdonságok | Példa a szerkesztésre |
|
|
| Tulajdonságok | Példa a szerkesztésre |
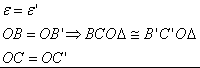 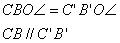
|
|
| Tulajdonságok | Példa a szerkesztésre |
|
|
| Tulajdonságok | Példa a szerkesztésre |
|
|
A háromszög területe
...az egyik oldal és a hozzátartozó magasság ismeretében
| Derékszögű háromszög esetén | Hegyesszögű háromszög esetén | Tompaszögű háromszög esetén |

|

|

|
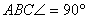 ABC háromszöget egy ezzel egybevágó
ACD háromszöggel egészítem ki, így egy téglalapot kapok. Ez esetben a téglalap területe: ABC háromszöget egy ezzel egybevágó
ACD háromszöggel egészítem ki, így egy téglalapot kapok. Ez esetben a téglalap területe:
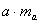 . Mivel két egybevágó háromszög
alkotja a téglalapot, a derékszögű háromszög területe . Mivel két egybevágó háromszög
alkotja a téglalapot, a derékszögű háromszög területe
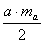 , tehát az alap és a
hozzátartozó magasság szorzatának a fele. , tehát az alap és a
hozzátartozó magasság szorzatának a fele.
|
Fölhasználom a derékszögű háromszög esetén bizonyítottakat:
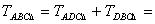
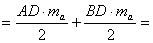
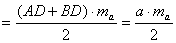 .
A hegyesszögű háromszög esetén (ugyanúgy, mint a derékszögű háromszögnél) .
A hegyesszögű háromszög esetén (ugyanúgy, mint a derékszögű háromszögnél)
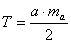 ,
tehát az alap és a hozzátartozó magasság szorzatának a fele. ,
tehát az alap és a hozzátartozó magasság szorzatának a fele.
|
Kiegészítem ABC háromszöget ADC háromszögre úgy, hogy az derékszög legyen.
Itt is felhasználom a derékszögű háromszög esetén bizonyítottakat.
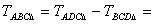
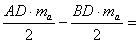
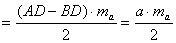 , tehát az alap és a hozzátartozó magasság szorzatának a fele.
, tehát az alap és a hozzátartozó magasság szorzatának a fele.
|
...a beírható kör sugarának és a kerület felének ismeretében

|
Jelöljük 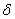 -val a beírt kör sugarát
és s-sel a kerület felét! DG CA-ra, DF CB-re és DE AB-re merőleges,
mivel DG, DF és DE a kör sugara, és ez érinti CA-t, CB-t és AB-t
(hiszen a kör érintője merőleges az érintési pontba húzott sugárra). Tehát GD ADC
háromszögnek, FD BCD háromszögnek és ED ABD háromszögnek a D-hez tartozó magasságvonala. -val a beírt kör sugarát
és s-sel a kerület felét! DG CA-ra, DF CB-re és DE AB-re merőleges,
mivel DG, DF és DE a kör sugara, és ez érinti CA-t, CB-t és AB-t
(hiszen a kör érintője merőleges az érintési pontba húzott sugárra). Tehát GD ADC
háromszögnek, FD BCD háromszögnek és ED ABD háromszögnek a D-hez tartozó magasságvonala.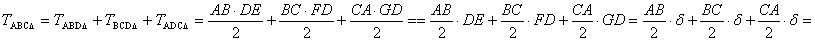
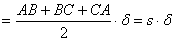 . .
|
(Az eljárásnál sehol sem használtuk, hogy a háromszög hegyesszögű,
derékszögű vagy tompaszögű, tehát minden háromszögre igaz ez a területképlet.)
Tehát a háromszög területe a kerület felének és a beírt kör sugarának szorzatával
(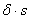 )
is megkapható. )
is megkapható.
|

|
Jelöljük 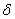 -val a CB oldalhoz
írt hozzáírt kör sugarát és s-sel a kerület felét! -val a CB oldalhoz
írt hozzáírt kör sugarát és s-sel a kerület felét!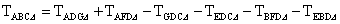 . Az egyenlet jobb oldalán mindegyik
háromszögnek D-hez tartozó magasságvonala: . Az egyenlet jobb oldalán mindegyik
háromszögnek D-hez tartozó magasságvonala: 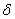 .
Ennek segítségével kiszámolható ABC háromszög területe: .
Ennek segítségével kiszámolható ABC háromszög területe: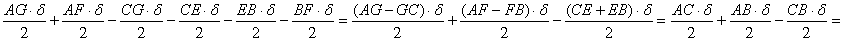
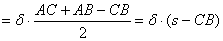
|
| Az eljárásnál sehol sem használtam, hogy a háromszög hegyesszögű, derékszögű vagy tompaszögű, tehát az összes típusú háromszögre alkalmazható az eljárás. Tehát a háromszög területe az alábbi módon is kiszámolható: a kerület feléből kivonok egy oldalt és ez beszorzom az ehhez tartozó hozzáírt kör sugarával. |
|
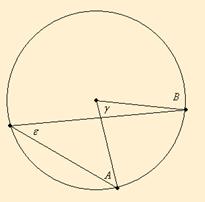
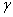 : AB-hez tartozó középponti szög. : AB-hez tartozó középponti szög.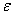 : AB-hez tartozó kerületi szög. : AB-hez tartozó kerületi szög.
Az AB-hez tartozó középponti szög 2-szerese az AB-hez tartozó kerületi szögnek.
Ennek bizonyításához vizsgáljuk meg a lehetséges eseteket!
|
||
|
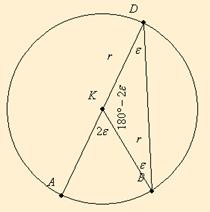
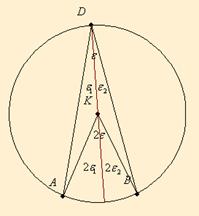
Mivel
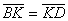 , a , a
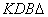 egyenlőszárú, így a egyenlőszárú, így a
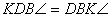 . Ebből kiszámítható . Ebből kiszámítható
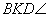 , majd ebből az , majd ebből az
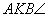 . .
|
|
Képzeletben fel kell osztani a szöget két olyan esetre, mint az első. Ebből már megkapjuk a szöget:
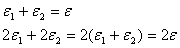
|
|
AB-hez
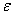 tartozik.
AC-hez tartozik.
AC-hez 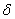 , AC középponti szöge az első eset alapján , AC középponti szöge az első eset alapján
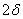 . BC-hez . BC-hez
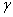 tartozik, BC középponti szöge az első eset alapján tartozik, BC középponti szöge az első eset alapján
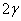 . .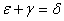 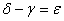 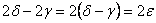
|
|
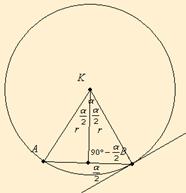
Ebben a különleges esetben a középponti szögtől kell indulni. Azt kell
felhasználni, hogy az egyenlőszárú háromszögben a szögfelező merőleges az oldalra.
|
Függvények
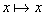
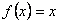
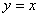
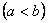 és
és
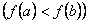 .
.
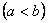 és
és
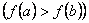 .
.
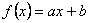 , ahol
, ahol
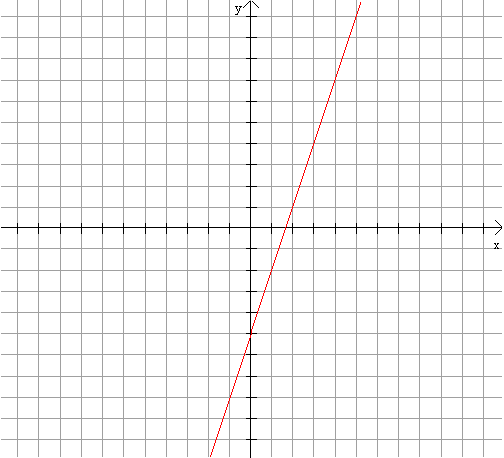
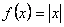 , ahol
, ahol
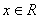
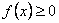
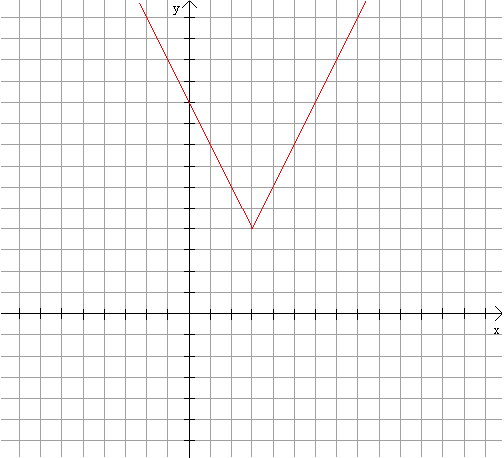
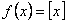

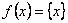
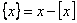

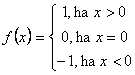

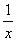 függvény egyenlete:
függvény egyenlete:
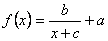 , ahol
, ahol
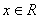 , ahol
, ahol
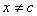
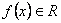 , ahol
, ahol
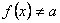
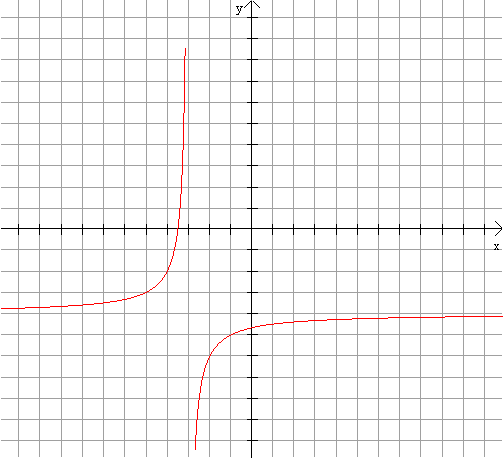
| 0. oszlop | ||||||||||||||||
| 0. sor | 1 | 1. oszlop | ||||||||||||||
| 1. sor | 1 | 1 | 2. oszlop | |||||||||||||
| 2. sor | 1 | 2 | 1 | 3. oszlop | ||||||||||||
| 3. sor | 1 | 3 | 3 | 1 | ||||||||||||
| 4. sor | 1 | 4 | 6 | 4 | 1 | |||||||||||
| 5. sor | 1 | 5 | 10 | 10 | 5 | 1 | ||||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||||
| 1 | 7 | 21 | 35 | 53 | 21 | 7 | 1 | |||||||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
A Fibonacci-sorozat összefüggése
| 1 | ||||||||
| 1 | 1 | |||||||
| 1 | 2 | 1 | ||||||
| 1 | 3 | 3 | 1 | |||||
| 1 | 4 | 6 | 4 | 1 | ||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
| 1. elem | ||||||||||
| 0. sor | 1 | 2. elem | ||||||||
| 1. sor | 1 | 1 | 3. elem | |||||||
| 2. sor | 1 | 2 | 1 | |||||||
| 1 | 3 | 3 | 1 | |||||||
| 1 | 4 | 6 | 4 | 1 | ||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
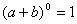 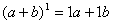 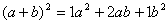 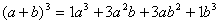  |
|