A CD matematikája

Az esszé anyagát nagyrészt a [vLint] és a [Philips] mûvek alapján állítottuk össze.

A pálya

A CD lejátszót a Philips és a Sony cég fejlesztette ki.

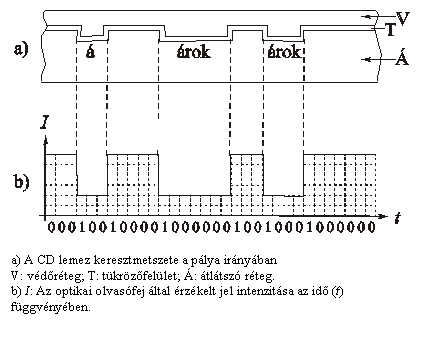
Maga a lemez egyetlen egy pályából áll, ami 5 km hosszú. Ezen binárisan van tárolva az információ. "Síkságok" és "árkok" követik egymást, de az árok alja is sík. Az 1-es bitet a változás, az árok széle, a 0-át az egységnyi hosszúságú vízszintes rész jelöli, amely lehet síkságon vagy az árok alján is.

A kódolt üzenetnek nagyon sok feltételt tudnia kell:

1) A digitalizálás ellenére az emberi fül számára hûen adja vissza a felvett zenét;
2) Az elszórt véletlenszerû bithibákat képes legyen kijavítani;
3) A csomóban keletkezõ hibák --- ujjlenyomatok, karcolások, anyaghibák --- korrigálását is megoldja;
4) A hallgató számára információt tudjon nyújtani, hogy hol tart;
5) A lézeres leolvasószerkezet hatékonyan olvasni tudja az információt;
6) A szerkezet mûködése ne keltsen az emberi fül számára hallható zajt (a lejátszandó zenén kívül).

Audiobit

A zene felvételekor az érzékelõ bizonyos idõnként "mintát vesz", azaz egy-egy pillanatban megméri milyen a beérkezõ hullám nyomása. Lényegében ez az érték a tárolt információ.

A felvétel lejátszásakor keletkezõ hang a pillanatnyi minták visszaadásából áll össze, így természetesen nem pont ugyanaz, mint amit fel szándékoztak venni. A mintavételezés gyakoriságától függõen, a zenei hang bizonyos hullámhosszú összetevõi hûen hallhatók.

Egy fizikai elv, Nyquist tétele, kapcsolatot teremt a mintavételezés gyakorisága, és az abból

hûen rekonstruálható hanghullámok frekvenciája között. Ennek a tételnek az alapján és abból kiindulva, hogy az emberi fül kb. 20 000 Hz-ig hall jól másodpercenként 44 100-nek adódik a szükséges mintavételezési gyakoriság.

Minden minta eredményét 16 bitté alakítja a rendszer. A felvétel általában sztereó, így máris

32 bit - úgynevezett audiobit - tartozik egyetlen pillanatnyi mintához. A 32 bit 4 byte-ba van rendezve (egy byte az nyolc egymást követõ bit).

2-hiba javító kód

Ha nem volnának hibajavító kódok hozzátéve a felvett audiobitekhez, akkor a CD lemez lejátszhatatlan minõségû lenne. A leggyakoribb "károkozók" az ujjlenyomatok,  az apró karcolások, a lemezben vagy rajta lévõ idegen anyagok, a mûanyagban óhatatlanul meglévõ légbuborékok, az eredeti felületi egyenetlenségek és a felvételkor vétett pontatlanságok.

Tegyük fel, hogy nem alkalmazunk hibajavító kódot. Ha a byte-hiba valószínûsége csupán 0,01% lenne, akkor az egy mintavételnek megfelelõ információban, azaz 4 byte-ban megbúvó hiba esélye 1-0,9999⁴≈0,9996 alapján kb. 0,04%-os lenne. Ez másodpercenként több mint 17 hibás lejátszott hangot okozna.

Tegyük fel elõször, hogy csak 1-hiba javítást alkalmazunk. A CD-n használt Reed-Solomon-féle kódolási eljárás egy-egy byte-ot egyben, egyetlen "számként" kezel. Ennek részleteibe most nem megyünk bele, inkább egyszerûsítésként képzeljük azt, mintha egy byte-on csak 31-féle információ lenne szállítható. Feleltessünk meg minden lehetõségnek egy 0 és 30 közötti számot és számoljunk velük mod 31.[1]

Az 1-hiba javítás megoldható úgy, hogy minden mintavételnek megfelelõ byte-négyeshez még 2 byte-ot veszünk hozzá. Az R-S kódolás ezt az 1.1 feladathoz kicsit hasonlóan oldja meg. Az x₁, x₂, x₃, x₄ eredeti byte-ok mellé az x₅ és x₆ ellenõrzõ biteket úgy kell választani, hogy teljesüljön az alábbi két összefüggés:

x₁ + x₂ + x₃ + x₄ + x₅ + x₆ ≡ 0 (mod 31), x₁ + 2x₂ + 3x₃ + 4x₄ + 5x₅ + 6x₆ ≡ 0 (mod 31).

Ha a dekódolásnál kiderül, hogy nem teljesül ez a két összefüggés, mondjuk a felsõ bal oldali kifejezés értéke 2, az alsóé pedig 41, azaz 10 (mod 31), akkor - abban bízva, hogy csak 1 hiba történt - kiszámolhatjuk a kódolt információt. Tudjuk, hogy a hiba értéke 2, tehát azt kell megkeresnünk, hogy melyik 1 és 26 közötti szám kétszerese ad 10 maradékot 31-gyel osztva. Ez a szám az 5, tehát az x₅ byte hibás, 2-vel nagyobb a kelleténél (mod 31).

Nézzük, most mennyi hibára számíthatunk! Sajnos azzal, hogy megnöveltük a bitsorozat hosszát vagy kevesebb zenét kell rögzítenünk a lemezen, vagy kisebb jeleket sûrûbben kell ír­nunk a CD-re, ami növeli a hiba valószínûségét. Az elsõ lehetõséget ne fogadjuk el. Tegyük fel, hogy a byte-hiba valószínûsége 0,02%-ra nõ. Annak esélye, hogy egy minta­vételnek meg­felelõ, most már 6 byte-ból álló adatsor hibás lesz, tehát 2 hiba kerül bele:

1-0,9998⁶ - 6·0,0002·0,9998⁵ ≈ 0,0000006.

Ez másodpercenként csak átlagosan kb. 0,0264 hibás lejátszott hangot okozna, ami lényege­sen jobb, mintha nem alkalmaztunk volna kódolást.

Egy, az elõzõnél jobb, két hibát javító kóddal még sokkal jobb eredményt érhetünk el. Most byte-négyesek helyett byte-ok nyolcas csoportjaira osztjuk a kódolandó üzenetet, és ezekhez négy további byte-ot illesztünk. Nevezetesen, az eredeti byte-oknak megfelelõ 8 szám legyen

x₁, x₂, ..., x₈, a négy ellenõrzõ szám pedig x₉, x₁₀, x₁₁, x₁₂. Szabályaink legyenek

x₁ + x₂ + x₃ + x₄ + ... + x₁₁ + x₁₂ ≡ 0 (mod 31), x₁ + 2x₂ + 3x₃ + 4x₄ + ... + 11x₁₁ + 12x₁₂ ≡ 0 (mod 31), x₁ + 4x₂ + 9x₃ + 16x₄ + ... + 121x₁₁ + 144x₁₂ ≡ 0 (mod 31), x₁ + 8x₂ + 27x₃ + 64x₄ + ... + 1331x₁₁ + 1728x₁₂ ≡ 0 (mod 31).

Annak részletes vizsgálatát, hogy így 2-hibajavító kódot kapunk, feladatnak hagyjuk. Jegyez­zük meg, hogy ebben az esetben is csak másfélszer annyi üzenetet kell átküldenünk, mint kódo­lás nélkül. Ha tehát itt is a 0,02%-os hibájú berendezést használjuk, akkor a legalább 3 hibát tartalmazó csoportok lesznek azok, amelyeket nem tudunk javítani. Ennek valószínûsége

1-0,9998¹² - 12·0,0002·0,9998¹¹ - 66·0,0002²·0,9998¹⁰ ≈ 0,000000002.

Ha úgy számolunk, hogy ilyenkor a 8 byte-hoz tartozó mindkét hang rossz, akkor is másod­percenként átlagosan csak kb. 0,0000774 hibás lejátszott hangot kapnánk, az egy órányi zene alatt összesen 0,28-at. Ez már elfogadható eredmény.

Lényeges, hogy a CD-n olyan kódot használjunk, amely a lehetõ legkisebb arányban növeli meg az adatsor hosszát, és nagyon gyorsan dekódolható.

"Keresztbe font" kódok

Eddig csak a véletlenszerû, elszórt hibák kiszûrésérõl volt szó. Sajnos, a hibák jelentõs része csomóban jelentkezik. Ezek ellenében a CD-n két "keresztbe font" (Cross-Interleaved) Reed-Solomon kód biztosítja az információ megmaradását.

Ez egyrészt azt jelenti, hogy az egymáshoz kapcsolódó információk a lemez különbözõ helyein vannak elhelyezve, az egymás mellé kerülõ jelek pedig a lejátszandó zenében valójában egymástól nagyobb idõkülönbséggel következnek. Így a hibafolt ugyan több információba "belepiszkít", de mindegyikbe csak egy picit.

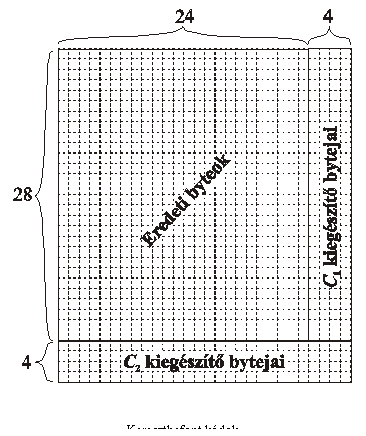
A másik trükk az, hogy a két kódolás az alábbi táblázatos formához hasonló módon mûködik együtt. Az elsõ, C1 kód 24 byte-ot kezel együtt, ezekhez 4 byte-ot tesz hozzá 2-hiba javító módon, tehát a létrejövõ 28 byte-os kódszavak minimális távolsága 5 lesz. Rendezzünk el 28 ilyen, már C1-gyel kódolt 28 byte-os adatsort egy táblázat soraiban! A második, C2 kód 28 byte-ot kezel együtt, a táblázat minden oszlopát további 4 byte-tal egészíti ki 2-hiba javító módon, tehát a létrejövõ 32 byte-os oszlopkódok minimális távolsága 5 lesz.

A két kód alkalmazásával lényegében egy 24×28-as táblázat adatait kódoltuk át egy

28×32-es táblázattá. Bebizonyítható, hogy az így létrejövõ táblázatok minimális távolsága 25, tehát a kettõs kód alkalmas a 28×32 adatban keletkezõ 12 hiba kijavítására.

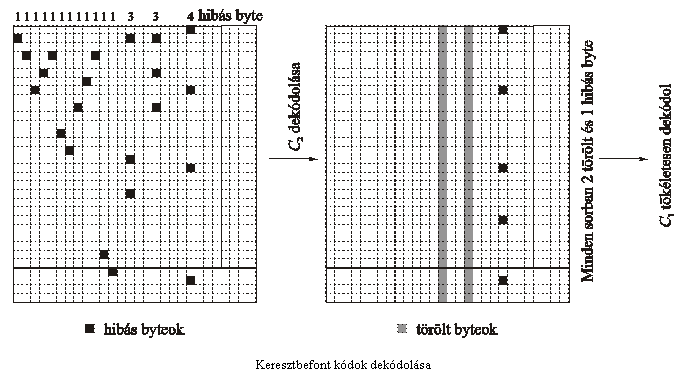
Képzeljünk el egy ennél sokkal rosszabb esetet, amikor 22 hiba van a táblázatban: tizenkét oszlopban 1-1 hiba, két oszlopban 3, egyben pedig 4 hiba is elõfordul. Nem várható el, hogy ki tudjuk javítani a hibákat, hiszen az oszlopok 2-hiba javítása után még elképzelhetõ, hogy marad sor 3 hibával. Úgy döntünk, hogy a C2 kódot a dekódolásnál csak 1-hiba javításra hasz­náljuk.

Fel tudjuk ismerni a 3 hibát tartalmazó oszlopokat, mert azok legalább 2 távolságra vannak a legközelebbi kódszótól. Könnyen elképzelhetõ viszont, hogy a 4 hibát tartalmazó oszlop csak 1 távolságra került egy kódszótól, így azt "kijavítjuk" 5 hibásra. A trükk az, hogy kijavítjuk (legalábbis így képzeljük) az 1 hibát tartalmazó oszlopokat, azokat viszont, amelyekrõl látjuk, hogy ennél több hibát tartalmaznak csak megjelöljük, hogy "törlendõ", ne vegyék figyelembe. Korábbi feladatainknak nyelvén a "hazugságot" "hanyagsággá" változtatjuk. Ez azt jelenti, hogy a 32 oszlopból C2 dekódolása után 29 jó, 2 törlendõ, 1-ben pedig 5 hiba is van. Nézzük most a sorokat, amelyeket C1-gyel kódoltunk! Mindegyikben 2 jel törölve van, öt sorban pedig van egy-egy hibás is. Mivel C1 minimális távolsága 5, így mindegyiket ki tudja javítani.

Elõfordulhat mégis, hogy a dekódoló észreveszi a hibát, de nem tudja kijavítani. Ez a helyzet pl. akkor, amikor túl sok legalább 2-hibás oszlop van. Ekkor a C2 dekóder végül is a "tör­len­dõ" jelet mellékeli jónéhány byte-hoz.

A dekóderbõl kimenõ byte-ok még mindig nem a lejátszás sorrendjében következnek egymás után, hanem összefonódva. A visszarendezéskor az "épségben" lévõ társai közé érkezõ "tör­len­dõ" byte helyettesíthetõ szomszédai átlagával. Ilyen interpolációval, ami szukcesszíven is alkalmazható elérhetõ, hogy ahelyett, hogy "mute"-ra kapcsolna a zenegép, egy-egy pilla­nat­ban amolyan "kitöltõ" hangot ad. Ez, ha tényleg csak pillanatokról van szó való­színûleg észre sem vehetõ.

A csomóhiba maximális hossza, amit a dekodolással még ki tud javítani a rendszer 4000 adatbit. Tehát ha ennyi egymást követõ bit elromlik, akkor azt nem fogjuk észrevenni. Ez a disc-en 2,5 mm-nyi torzulást jelent a pálya irányában.

Az interpoláció segítségével pótolható egybefüggõ bitsorozat maximális hossza 12 000.

A barázda-jelek

Láttuk, hogy a mintavételbõl keletkezõ byte-ok 24-es csoportját az egyik kód 28, majd a másik 32 byte hosszúságúra növeli. (A "keresztbe fonás" miatt ez ennél valamivel bonyolultabb, csak a számarányok tekintetében pontos a megállapítás.) A 32 byte-hoz hozzátesznek egy 33.-at, egy kontrol byte-ot, amely lehetõvé teszi, hogy tudjuk, hogy hol tartunk.

Az így kapott adatsor nem alkalmas arra, hogy a "síkságok" és "árkok" módszerével az anyagba vive, azt a lézer olvasófej biztonságosan ki tudja olvasni. Az árok mélysége és a síkság magassága úgy van beállítva, hogy az árokból sokkal kisebb intenzitású fény verõdik vissza a leolvasófejbe, mint a síkságról. Az egymáshoz túl közeli 1-esek, tehát közeli falak, olyan interferenciát okoznának, amely megzavarná a leolvasást. A túl távoli falak esetén nagy a bizonytalanság, hogy pontosan mennyi ideje tart a lapos rész, hány 0-t jelent ez. Ilyen megfontolások alapján a lemezen olyan jelsorozatokat érdemes tárolni, amelyben két 1-es között legalább két, de legfeljebb tíz 0 van. Az ilyen elrendezésû jelsorozatok a barázda-jelek (channel-bits).

A byte-ok 256 lehetséges értékét hány barázda-biten lehet tárolni? Ennek meghatározásához a mérnököknek az alábbi feladatot kellett megoldaniuk:

Ha F_n az n hosszúságú barázda-jelek száma, akkor melyik az a legkisebb n érték, amelyre F_n ≥ 256?

A helyes eredmény 14. Tehát a byte-okat 14 bitre bõvítik. Ez az eljárás az EFM átalakítás (Eight-to-Fourteen Modulation).

Problémát okoz, hogy két szomszédos barázda-jel együtt már nem feltétlenül teljesíti a baráz­da-jelekre kirótt követelményeket. Segítséget jelent viszont, hogy F₁₄ értéke 267, tehát 11 darab 14 hosszúságú barázda-jel kidobható. 10-et azért hagytak ki, mert "nem jöttek volna jól ki a szomszédaikkal", 1-et pedig véletlenszerûen választottak. Ezután az EFM átalakítást úgy tervezték meg, hogy a szükséges logikai kapuk száma minimális legyen.

Az egymás mellé kerülõ barázda-jelek problémáját nem teljesen oldotta meg a 10 kellemetlen sorozat kidobása. További 3-3 bitet kellett berakni a byte-oknak megfelelõ 14 hosszúságú bit­so­rozatok közé.

A 3 bit egy kicsit túlbiztosított. Beállításukkor arra is törekednek, hogy a pálya kezdetétõl a síkságok és az árkok hosszának különbsége minél kisebb legyen. Az ezt a különbséget leíró hullámszerû függvényt ugyanis a berendezés "érzi": annak megfelelõ zaj indukálódik a berendezésben. Ebbõl ki kell küszöbölni az emberi fül számára hallható nagyobb amplitudójú komponenseket, tehát minél kisebb kitéréseket kell elérni.

Végül a 33 byte-ból adódó 33×17 bit után 27 szinkronizáló bit jön. Ez a 27 bitsorozat olyan, hogy nem keverhetõ össze a kódolt zenével, csak arra szolgál, hogy az egyik 33-as egység végét, a következõ kezdetét jelölje.

Mindebbõl kiszámolható, hogy egyetlen másodpercnyi zenét 4 321 800 biten tárol a CD.