Megoldás
(Alsó korlát)
Tegyük fel, hogy k előre leírt kérdéssel ki lehet találni a gondolt számot.
Tekintsük ezt a k kérdést, és válasszuk ki a 16 szám egyikét, mintha az
lenne a gondolt szám. Válaszoljuk meg a k db kérdést hazugság nélkül.
Írjunk 0-t az "igen", 1-est a "nem" válasz helyett. Így egy
k hosszúságú 0-1 sorozatot kapunk, amit a kiválasztott szám kódjának
fogok nevezni. Ha a válaszoló egyszer hazudik, akkor nem a szám kódját kapjuk,
hanem egy olyan sorozatot, amely egy helyen különbözik a szám kódjától. Az
ilyen sorozatokat a szám álkódjának fogom nevezni. Álkódból éppen k
darab van, mert a k kérdésből egyre kaphatunk rossz választ, és
mindegyik kérdésre egyféle rossz választ kaphatunk. A 16 számhoz 16 kód és 16k
álkód tartozik. Ezeknek mind különbözőeknek kell lennie, mert ha volna közös
elemük, akkor az annak a 0-1 sorozatnak megfelelő válaszok esetén nem tudnánk
kitalálni a gondolt számot. Összesen 2k darab k hosszú
0-1 sorozat van, így biztosan teljesül a 16·(k+1) ≤
2k egyenlőtlenség. A két oldal értékét k = 1, 2, ... esetén
táblázatban írom fel.
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 16· (k+1) | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 |
| 2k | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
Látható, hogy az egyenlőtlenség a k = 7 esetben teljesül először. Tehát legalább 7 előre leírt kérdésre van szükség.
I. konstrukció
("Mohó algoritmus")
7 előre leírt kérdéssel megoldható a feladat.
Ennek igazolásához
16 db olyan 7 hosszúságú 0-1 sorozatot kell megadni, amelyek közül bármelyik
kettő legalább három helyen eltér egymástól. Ebből ugyanis következik, hogy a
16 kód és 16·7 álkód mind különböző lesz: ha két
különböző kódhoz tartozó álkód megegyezik, akkor a két kód csak két helyen tér
el egymástól.
Mohó algoritmussal dolgozunk. A 0000000 sorozattól kezdve a lexikografikusan
legkisebb olyan sorozatot keressük, amelyik mindegyik korábban már kiválasztott sorozattól legalább 3 helyen különbözik. Az
eredményül kapott 16 db 0 - 1 sorozat
az alábbi táblázat oszlopaiban található:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 1. sor | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2. sor | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 3. sor | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 4. sor | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 5. sor | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 6. sor | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 7. sor | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
A 7 kérdés a 7 sorból olvasható ki. Egy oszlophoz tartozó kérdés, azokra az 1 és 16 közti számokra kérdez rá, amelyek sorában az adott oszlopban 0 áll. A hét kérdés mindegyike így kezdődik: "A gondolt szám az itt megadott halmazban van?". A hét megadott halmaz az alábbi sorokban olvasható:
| 1. kérdés: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||||||
| 2. kérdés: | 1 | 2 | 3 | 4 | 9 | 10 | 11 | 12 | ||||||||
| 3. kérdés: | 1 | 2 | 5 | 6 | 9 | 10 | 13 | 14 | ||||||||
| 4. kérdés: | 1 | 2 | 7 | 8 | 11 | 12 | 13 | 14 | ||||||||
| 5. kérdés: | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | ||||||||
| 6. kérdés: | 1 | 3 | 6 | 8 | 10 | 12 | 13 | 15 | ||||||||
| 7. kérdés: | 1 | 4 | 5 | 8 | 10 | 11 | 14 | 15 |
Érdekes, hogy a fenti 1., 2., 3., 5. kérdések rendre megegyeznek az 5.8 b) feladatra adott megoldások kérdéseivel (lásd a 16. szakkört).
II. konstrukció
(Algebra I.)
Az 5.8 b) feladatra adott II. konstrukcióra építve az 1.2 feladat IV. megoldásának
mintájára dolgozunk.
Legyen (n-1)
kettes számrendszerbeli alakja x8x4x2x1
(ahol n befutja az {1, 2, ..., 16} halmazt, míg xi értéke 0 vagy 1). Ebben a megközelítésben az 5.8 b) feladatra adott II. konstrukció
kérdései így írhatók:
Állítjuk, hogy a jelen feladat megoldását kapjuk, ha a fenti négy kérdést kiegészítjük az alábbi hárommal:
ahol az összeadás és az egyenlőség mindenütt mod 2 értendő.
A válaszokat elfogadva megállapíthatjuk x8, x4, x2, x1, x4+x2+x1, x8+x2+x1, x8+x4+x1 értékeit és az első négyre kapott értékkel leellenőrizhetjük az utolsó hármat. Ha egyik ellenőrzés sem teljesül, akkor biztosan x1 volt a ludas, értékét kijavíthatjuk. Ha két ellenőrzésnél sem stimmelt az összeg, akkor x2, x4 vagy x8 értéke volt hibás, attól függően, hogy melyik két egyenlettel volt baj. Mindegyik változó legalább két összegben szerepel, így ha csak egy ellenőrzésnél jutottunk ellentmondáshoz, akkor biztosan annak az összegnek az értékét kaptuk rosszul, a változók értékei helyesek. Végül, ha minden ellenőrzés klappolt, akkor nem is kaptunk hamis választ, tudjuk a változók értékeit.
Megjegyzés: mutassuk meg, hogy az I. konstrukcióban megadott kérdések is megfogalmazhatók a II. konstrukcióban adott algebrai alakban!
III. konstrukció
(Algebra II., Hamming kód)
Az I. konstrukció gondolatmenete alapján, de a II. konstrukcióban szereplő algebrai
módszerhez hasonló megoldást keresünk.
16 db olyan hét hosszúságú 0 - 1 sorozatot kell megadni, amelyek közül bármelyik kettő
legalább három helyen eltér egymástól. Szeretnénk ezeket a sorozatokat egy
homogén lineáris egyenletrendszer megoldásaként előállítani. (Itt, és az alábbiakban a +, ˇ műveletek és az egyenlőség is mod 2 értendő, az együtthatók, változók értékei 0 és 1 lehetnek.) Azaz olyan a1, a2, ..., a7, b1, b2, ..., b7, c1, c2, ..., c7 együtthatókat keresünk, amelyek esetén a fenti egyenletrendszert kielégítő y1 y2 ... y7 sorozatok közül bármelyik kettő legalább 3 helyen eltér egymástól. Az ilyen kódot lineáris kódnak nevezik.
A lineáris kódnak a következő előnye van. Az egyenletrendszer egyik megoldása, tehát az egyik kódszó a 00...0 sorozat. Tegyük fel, hogy sikerül olyan az egyenletrendszer együtthatóit úgy megválasztani, hogy bármelyik másik megoldás 00...0-tól legalább három helyen térjen el, azaz legalább három 1-es legyen benne. Állítjuk, hogy ebben az esetben bármelyik két megoldás legalább három helyen eltér egymástól. Valóban, ha az y11 y21 ... y71 és az y12 y22 ... y72 sorozat is teljesíti a fenti egyenletrendszert, azaz
akkor a megfelelő egyenletek kivonása révén kapjuk, hogy
azaz az (y11 - y12) (y21 - y22)... (y71 - y72) sorozat is teljesíti az eredeti egyenletrendszert. Ebben a sorozatban feltételünk szerint legalább három 1-es van, de pontosan ott van benne 0-tól különböző szám, ahol az y11 y21 ... y71, y12 y22 ... y72 sorozatok eltérnek egymástól. Tehát ha egy lineáris kódban nincs olyan kódszó, amelyikben egy vagy két 0-tól különböző jel van, akkor bármely két kódszó távolsága legalább három.
Feltételi egyenlet nélkül az y1, y2, ..., y7 bináris változók értékei 27-féleképpen választhatók meg, hiszen mind a hét változó szabadon és egymástól függetlenül fölveheti a 0, 1 értékek bármelyikét. Egy egyenlet lehetőséget ad, hogy az egyik változót kifejezzük a többiből, így a szabad változók száma eggyel csökken. Azt szeretnénk elérni, hogy az egyenletrendszernek 16 = 24 megoldása legyen, ehhez 3 (független) egyenletet kell megadni.
Az
egyenletrendszer tehát pontosan akkor megfelelő, ha (egyenletei függetlenek és) nincs olyan megoldása, amelyben az ismeretlenek közül egynek vagy kettőnek az értéke 1-es (és a többi 0).
y1 = 1, y2 = ... = y7 = 0 pontosan akkor megoldása a fenti egyenletrendszernek, ha az
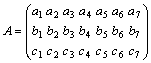
mátrix első oszlopában mindenütt 0 áll. Általában, egyenletrendszerünknek pontosan akkor van olyan megoldása, amelyben az egyik változó értéke 1, a többié 0, ha A-nak van azonosan 0 oszlopa.
y1 = y2 = 1, y3 = ... = y7 = 0 pontosan akkor megoldása az egyenletrendszernek, ha az A mátrix első két oszlopa egyenlő egymással. Általában, pontosan akkor van olyan megoldás, amelyben két változó értéke 1, a többié 0, ha A-nak van két egyforma oszlopa. Az A mátrix tehát pontosan akkor ad megfelelő egyenletrendszert, ha egyik oszlopa sem egyezik meg az azonosan 0 oszloppal vagy egy másik oszloppal (és az egyenletek függetlenek).
A egy-egy oszlopa egy három elemből álló bináris sorozat, amely 23 = 8-féleképpen választható meg. A 8 közül az egyik azonosan 0, ez nem lehet A-ban, tehát A oszlopai - a sorrendtől eltekintve - egyértelműen meghatározottak:
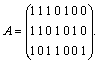
Tehát a megfelelő egyenletrendszer:
Ennek valóban 16 megoldása van (azaz egyenletei függetlenek) hiszen y1, y2, y3, y4 értékei szabadon választhatók és
A 16 megoldás itt látható:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| y1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| y2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| y3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| y4 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| y5 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| y6 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| y7 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
Látható, hogy - két sor felcserélődésétől eltekintve - ugyanahhoz a táblázathoz jutottunk, mint az I. konstrukció esetén.
Megjegyzés:
Az előbb látottak alapján új konstrukciót adunk a múlt órai 4.6, 5.6
példákhoz. Most tehát háromféle jelünk van, pld 0, 1, 2 és négyes sorozatokat
kell gyártanunk. Számoljunk mod 3 (tehát 2 = -1), és keressünk olyan
alakú egyenletrendszert, amely megoldáshalmaza 1-hiba javító lineáris kód! Azért van szükség most csak két egyenletre, mert 4 változónk van, de 9 kódszót keresünk, tehát két szabad változót kell hagynunk, kettőt kell tudni kiküszöbölni az egyenletekkel. Most is úgy kell megválasztani az egyenletrendszer együtthatóinak
mátrixát, hogy az egyenletrendszernek ne legyen olyan megoldása, amelyben csak egy vagy két változó értéke különbözik 0-tól. Az egy darab 0-tól különböző elemet tartalmazó sorozatokat most is úgy tudjuk kizárni, hogy nem engedünk meg a mátrixban olyan oszlopot, amelyben mindkét elem 0. Tekintsünk most két darab nullától különböző elemet tartalmazó sorozatokat, legyen pld y1 = y2 ≠ 0, y3 = y4 = 0. Ez pontosan akkor megoldás, ha a1 = - a2 és b1 = - b2, azaz ha az
oszlopvektorok egymás ellentettjei. Az y1 = 1, y2 = -1, y3 = y4 = 0 valamint az y1 = -1, y2 = 1, y3 = y4 = 0 számnégyesek pontosan akkor megoldások, ha a1 = a2 és b1 = b2, azaz ha
Ha nem akarunk olyan megoldásokat, amelyek legfeljebb két helyen térnek el egymástól, akkor olyan A mátrixot kell választani, amelynek nincsenek azonosan 0, egymással egyenlő, illetve egymással ellentétes oszlopai. Pld egy ilyen mátrix:
amely az
egyenletrendszert, azaz a
összefüggéseket határozza meg. Épp ezeket "találtuk ki" az előző órán a 4.6 feladat II. megoldásában.
IV. konstrukció
(Négyzetminta)
Térjünk
vissza a "Négyzetminta" feladathoz, az előző
foglalkozás első példájához! Egész számok helyett számoljunk binárisan
(mod 2), azaz a "páros" és "páratlan" szavakat 0 és 1
helyettesítse! A négyzet csúcsaihoz írt 8 számot 16-féleképpen adhatjuk meg,
hiszen a csúcsokhoz először írt egy-egy szám összesen 24-féle lehet
és ezek már meghatározzák a további négy számot. Így tehát összesen 16 db 0-1
sorozatot kapunk, amelyek egy lineáris halmazt alkotnak, azaz a 16 közül bármelyik
két sorozat összege (természetesen koordinátánként és mod 2 értve) is a 16
sorozat között van. A "Négyzetminta" feladatban azt láttuk, hogy e
sorozatokban 0, 4 vagy 8 db 1-es lehet, tehát a 16 sorozat egy olyan lineáris
kódot alkot, amelynek minimális távolsága 4. Ha a nyolcelemű sorozatok egyik,
pld az utolsó elemét mindegyikben elhagyjuk, akkor 16 olyan hételemű 0-1 sorozatot
kapunk, amelyek közül bármelyik kettő Hamming távolsága legalább 3. Az I. konstrukció
elején leírtak szerint éppen ilyen sorozatokat kerestünk.