A 'C'-sek Lexikona
|
Geometria I.
Pithagorasz-tétel |
Kombinatorika Permutáció: Kombináció Variáció |
Valószínűségszámítás |
|
Geometria II.
Fauerbach-kör |
Feladatok |
|
|
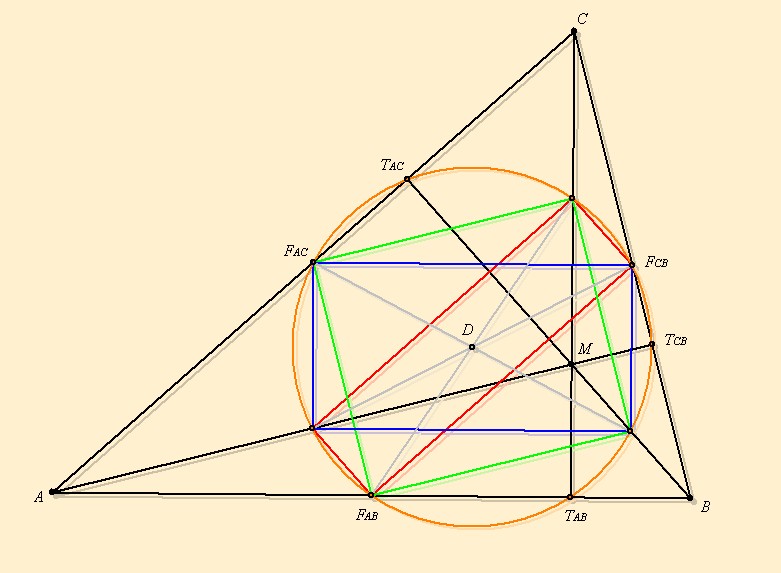
A háromszög oldalfelező pontjai, a magasságvonalainak
talppontjai, és a magasságpontot a csúcsokkal összekötő szakaszok
felezőpontjai egy körön vannak.
|
 |
Rajzoljuk be AMBC, ACMB és ABCM négyszögek oldalfelező pontjai által meghatározott négyszögeket. Az így kapott kék, zöld és piros négyszögek téglalapok, amit a következőből láthatjuk be:
| Ha behúzzuk egy négyszög oldalainak felezőpontjai által meghatározott négyszöget, akkor egy paralelogrammát kapunk. |
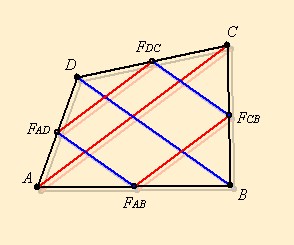 |
Bizonyítás (Ennek a betűzésnek nincs köze a fentihez.)
|
Ebben az esetben ez a paralelogramma egy téglalap, mivel a
négyszög átlói merőlegesek egymásra (az egyik az ABC háromszög
egyik oldala, a másik az ehhez az oldalhoz tartozó magasság).
A Thalesz-tétel megfordításból következően a téglalap átlói
felezve metszik egymást. Tehát a csúcsai egy körön vannak. Mivel
a 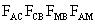 , ,
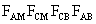 és és
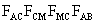 téglalapok
közül bármelyik kettőnek van egy közös átlója. Tehát ez a hat
pont egy körön van, melynek középpontja az átlók metszéspontja.
Ez a Feuerbach-kör. téglalapok
közül bármelyik kettőnek van egy közös átlója. Tehát ez a hat
pont egy körön van, melynek középpontja az átlók metszéspontja.
Ez a Feuerbach-kör. 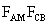 -re,
mint átmérőre emeljünk Thalesz-kört. A Thalesz-tétel megfordítása
következtében ezen a körön -re,
mint átmérőre emeljünk Thalesz-kört. A Thalesz-tétel megfordítása
következtében ezen a körön 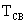 rajta lesz, mert
rajta lesz, mert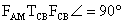 .
Hasonló alapon .
Hasonló alapon 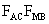 átmérőjű körön
átmérőjű körön 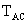 ,
az ,
az 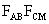 átmérőjű körön
átmérőjű körön 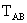 rajta lesz. Az előbb említett három kör megegyezik, mert mindhárom
egybeesik a Feuerbach-körrel. Így ezen a körön vannak a háromszög
oldalfelező pontjai, a magasságvonalainak talppontjai, és a
magasságpontot a csúcsokkal összekötő szakaszok felezőpontjai.
rajta lesz. Az előbb említett három kör megegyezik, mert mindhárom
egybeesik a Feuerbach-körrel. Így ezen a körön vannak a háromszög
oldalfelező pontjai, a magasságvonalainak talppontjai, és a
magasságpontot a csúcsokkal összekötő szakaszok felezőpontjai.
|
Két síkidom hasonló egymáshoz, ha egybevágósági transzformációkkal és középpontos hasonlósággal egymásba vihetőek.
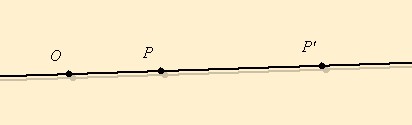 |
O: középpont, 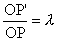 |
Tulajdonságai:
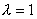 , mert ekkor minden ponz fix.)
, mert ekkor minden ponz fix.)
.gif) -szeresére változik
-szeresére változik
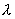 -szorosára változik
-szorosára változik
A fenti tulajdonságokat először belátom 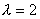 -re: -re: |
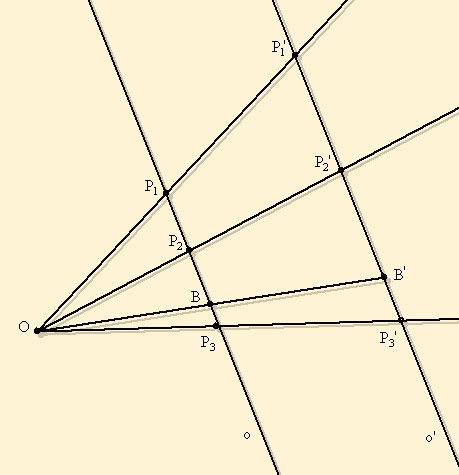 |
Az o egyenesen kiválasztik két pontot,
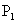 -t
és -t
és 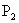 -t.
Ezekre a pontokra elvégezzük a -t.
Ezekre a pontokra elvégezzük a 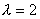 -szeres
nagyítást, így megkapjuk -szeres
nagyítást, így megkapjuk 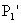 -t
és -t
és 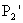 -t.
Húzzuk be ennek az egyenesét! (Fontos, hogy erről az egyenesről
nem állítjuk, hogy o' pontjai.) -t.
Húzzuk be ennek az egyenesét! (Fontos, hogy erről az egyenesről
nem állítjuk, hogy o' pontjai.) 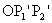 háromszögnek a
háromszögnek a 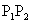 a középvonala, mert
a középvonala, mert 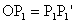 és
és 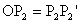 .
Ezért .
Ezért 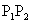 egyenese párhuzamos
egyenese párhuzamos 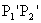 egyenesével.
egyenesével. Most a 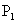 pont mellé az oegyenesen a
pont mellé az oegyenesen a 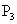 pontot veszem föl. A fentiekhez hasonlóan
pontot veszem föl. A fentiekhez hasonlóan 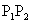 egyenese párhuzamos
egyenese párhuzamos 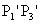 egyenesével.
egyenesével. 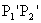 és
és 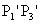 egyeneseknek van közös pontja,
egyeneseknek van közös pontja, 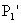 ,
és mindkettő párhuzamos ,
és mindkettő párhuzamos 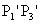 egyenesére. Mivel az Euklideszi-geometriában egy adott ponton
át egy adott egyenessel csak egy párhuzamos húzható, ezért
egyenesére. Mivel az Euklideszi-geometriában egy adott ponton
át egy adott egyenessel csak egy párhuzamos húzható, ezért
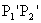 egyenes egybeesik
egyenes egybeesik 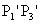 . .
Az előzőekből következően o egyenes minden pontja egy vele párhuzamos o' egyenesbe megy (ez 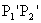 egyenese). Még azt kell belátni, hogy o' egyenes minden
pontja az o egyenes pontjainak képe.
egyenese). Még azt kell belátni, hogy o' egyenes minden
pontja az o egyenes pontjainak képe. Fölveszek o'-n egy B' pontot. Ezt összekötöm O-val. Mivel 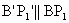 és
és 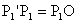 ,
ezért az ,
ezért az 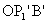 háromszög középvonalából következően
háromszög középvonalából következően 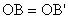 . .
Tehát  -re
egyenes képe vele párhuzamos egyenes lesz, szakasz képe pedig
vele párhuzamos és akkora lesz. -re
egyenes képe vele párhuzamos egyenes lesz, szakasz képe pedig
vele párhuzamos és akkora lesz. |
Most lássuk be 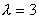 -ra!
-ra!
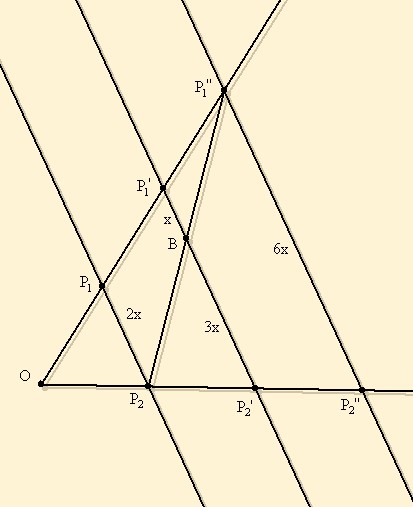 |
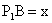
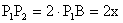 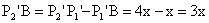 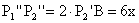 Tehát 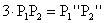 .
A .
A 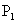 pontot rögzítem, és
pontot rögzítem, és 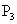 ,
... pontokat veszek föl. Erre a fönti levezetés ugyanígy megcsinálható.
Tehát ,
... pontokat veszek föl. Erre a fönti levezetés ugyanígy megcsinálható.
Tehát 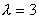 -ra
egyenes képe vele párhuzamos egyenes, szakasz képe pegig vele
párhuzamos, és 3-szor akkora. -ra
egyenes képe vele párhuzamos egyenes, szakasz képe pegig vele
párhuzamos, és 3-szor akkora. (Ezt a gondolatmenetet lehetne folytatni 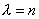 -re,
és ugyanezeket kell majd fölhasználni.) -re,
és ugyanezeket kell majd fölhasználni.)
|
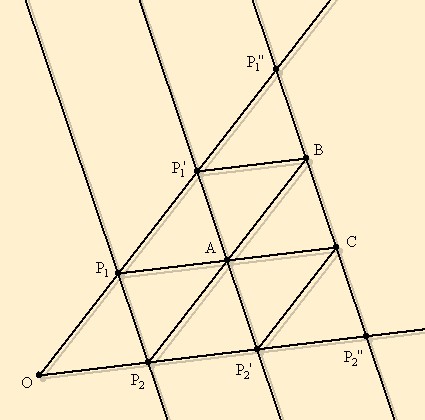
Majd 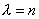 -re!
-re!
 |
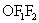 háromszöggel
úgytapétázom ki síkot, hogy mindig a középpontjára tükrözöm
(például háromszöggel
úgytapétázom ki síkot, hogy mindig a középpontjára tükrözöm
(például 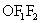 háromszöget
háromszöget 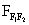 -re
tükrözve ABC háromszöget kapjuk). -re
tükrözve ABC háromszöget kapjuk). Elnevezem a szögeket. Legyen 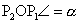 , ,
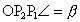 és
és 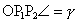 !
Ebből következően !
Ebből következően 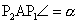 , ,
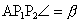 , ,
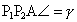 , ,
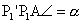 , ,
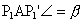 , ,
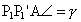 , ,
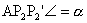 , ,
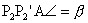 , ,
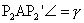 ...
Mivel ...
Mivel 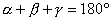 ,
ezért ,
ezért 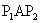 egy egyenesen van.
egy egyenesen van. Ugyanezen az elven 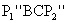 ,
... is egy egyenesen van. ,
... is egy egyenesen van. A 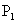 pontot rögzítem, és
pontot rögzítem, és 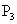 ,
... pontokat veszek föl, ezekre ugyan az bebizonyítható. Az
egyállású szögekből következően a nagyítás párhuzamos egyenest
ad. ,
... pontokat veszek föl, ezekre ugyan az bebizonyítható. Az
egyállású szögekből következően a nagyítás párhuzamos egyenest
ad. Tehát a 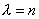 -szeres
nagyításnál szakasz képe vele párhuzamos és n-szerese. -szeres
nagyításnál szakasz képe vele párhuzamos és n-szerese.
|
Majd végül 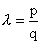 -ra! -ra!
Ez a nagyítás egyenlő egy p-szeres nagyítással és egy q-szoros kicsinyítéssel (p és q egész számok). Ezekre már fönt bizonyítottuk a tulajdonságokat, tehát ezek racionális nagyításnál is igazak. |
Két háromszög hasonló egymáshoz, ha:
Ha egy szög szárait párhuzamosokkal metsszük, akkor az egyik száron keletkező szakaszok aránya megegyezik a másik száron keletkező megfelelő szakszok arányával.
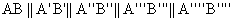
A fent bizonyítottak alapján AB-t egy-egy nagyítással A'B'-be, A''B''-be, A'''B'''-be, A''''B''''-be, ... lehet juttatni. Tehát
,
,
,
,
Ebből következően,
ami így is írható:.
,
,
... Hasonlóan bármely két párhuzamos szelőrő be lehet látni, hogy egyenlő-vel, tehát egymással is egyenlőek. Így bebizonyítottuk a tételt.
Magasságtétel, befogótétel, Pithagorasz-tétel
Egy derékszögű háromszögbe a derékszögből behúzom a magasságot, majd elnevezem a szögeket.
,
,
,
,
,
,
.
Mivel mind a három háromszögben minden szög megegyezik, ezért ezek hasonlóak..
Ezekből az arányokat átírva:
a : b : c = m : q : b = p : m : a
Ebből kiválasztom a következő arányt:
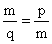
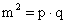
Magasságtétel
Egy derékszögű háromszögben a derékszögből kiinduló magasságvonal hossza az átfogóból az általa kiszelt két szakasz mértani közepe.
Másik két aránypárt kiválasztva:
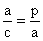
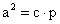
Majd másik kettőt, ami lényegében ugyan ez:
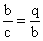
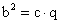
Befogótétel
Egy derékszögő háromszög egyik befogója egyenlő a derékszögből kiinduló magasságvonal által levágott vetületének és az átfogó mértani közepével.
Pithagorasz-tétel
Egy derékszögő háromszögben a két befogó négyzetének összege egyenlő az átfogó négyzetének összegével.
A fentiekből tudjuk, hogy,
,
valamint azt, hogy.
Így.
|
|
Állítás Az állítás a Pitagorasz-tétel másik megfogalmazásával geometriai úton is bizonyítható. E szerint a derékszögű háromszög befogóira rajzolt négyzetek területének összege az átfogóra rajzolt négyzet területével egyenlő. Ennek belátásához daraboljuk fel az alábbiak szerint az a+b oldalú négyzetet. |
Kombinatorika
| Valószínűségszámítás Kísérlet: Vannak olyan jelenségek, amiket sokszor meg tudunk figyelni. Ilyen például a lottóhúzás. Egy ilyen megfigyelést szoktak ,,kísérletnek'' is nevezni. |
| Valószínűség: B egy tetszőleges esemény valószínűsége: 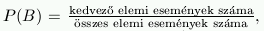 ahol kedvező elemi esemény az, ami esetén a B esemény bekövetkezik. Tulajdonságai: Minden A eseményre 0 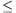 P(A) P(A)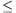 1.
1.P(biztos esemény)=1, P( 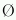 )=0
)=0 |