(Feladat azonosítója: OKTV_20232024_1k2f5f )
Témakör: *Geometria
Adott a síkon az $ e $ és az $ f $ egyenes, valamint az ábrának megfelelően az $ ABE $, $ BCF $, $ CDG $ szabályos háromszög ($ A, B, C, D \in e$ és $E, F, G \in f$ ), ahol a háromszögek oldalai rendre $ a $, $ b $ és $ c $ ($ a < b < c$).
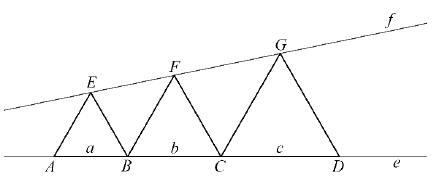
a) Igazolja, hogy $ b^2 = ac $.
b) Igazolja, hogy az a, b és c oldalakból pontosan akkor szerkeszthető háromszög, ha
$ 1<\dfrac{c}{a}<\dfrac{3+\sqrt{5}}{2}$
Megoldás:
a) Igaz az állítás
b) Igaz az állítás